Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
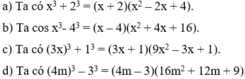
a: \(x^3+27=\left(x+3\right)\left(x^2-3x+9\right)\)
b: \(x^3-\dfrac{1}{8}=\left(x-\dfrac{1}{2}\right)\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)\)
c: \(8x^3+y^3=\left(2x+y\right)\left(4x^2-2xy+y^2\right)\)
a) \(\left(x+3\right)\cdot\left(x^2-3x+9\right)\)
b) \(\left(x-\dfrac{1}{2}\right)\cdot\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)\)
c) \(\left(2x+y\right)\cdot\left(4x^2-2xy+y^2\right)\)
a) \(8y^3+1\)
\(=\left(2y\right)^3+1^3\)
\(=\left(2y+1\right)\left(4y^2-2y+1\right)\)
b) \(y^3-8\)
\(=y^3-2^3\)
\(=\left(y-2\right)\left(y^2+2y+4\right)\)
`8y^3 + 1 = (2y+1)(4y^2 - 2y + 1)`
`y^3 -8 =(y-2)(y^2+2y+4)`
a: \(\left(x+y+z\right)^2-\left(y+z\right)^2\)
\(=\left(x+y+z-y-z\right)\left(x+y+z+y+z\right)\)
\(=x\left(x+2y+3z\right)\)
b: \(\left(x+3\right)^2+4\left(x+3\right)+4\)
\(=\left(x+3+2\right)^2\)
\(=\left(x+5\right)\left(x+5\right)\)
c: \(25+10\left(x+1\right)+\left(x+1\right)^2\)
\(=\left(x+1+5\right)^2\)
\(=\left(x+6\right)\left(x+6\right)\)
\(1,\\ a,=\left(x+2\right)\left(x^2-2x+4\right)\\ b,=\left(x-4\right)\left(x^2+8x+16\right)\\ c,=\left(3x+1\right)\left(9x^2-3x+1\right)\\ d,=\left(4m-3\right)\left(16m^2+12m+9\right)\\ 2,\\ a,=x^3+125\\ b,=1-x^3\\ c,=y^3+27t^3\)
a)
\(=\left(x+2\right)\left(x^2-2x+4\right)\)
b)
\(=\left(x-4\right)\left(x^2+4x+16\right)\)
c)=\(\left(3x+1\right)\left(9x^2-3x+1\right)\)
d)
=\(\left(4m-3\right)\left(16m^2+12m+9\right)\)
a: \(8x^3-1=\left(2x-1\right)\left(4x^2+2x+1\right)\)
b: \(x^3+8y^3=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)
c: \(x^3+125=\left(x+5\right)\left(x^2-5x+25\right)\)
d: \(x^3-27y^3=\left(x-3y\right)\left(x^2+3xy+9y^2\right)\)
a) 8x3 - 1
= (2x)3 - 13
= (2x - 1)(4x2 + 2x + 1)
b) x3 + 8y3
= x3 + (2y)3
= (x + 2y)(x2 + 2xy + 4y2)
c) x3 + 125
= x3 + 53
= (x + 5)(x2 - 5x + 25)
d) x3 - 27y3
= x3 - (3y)3
= (x - 3y)(x2 + 3xy + 9y2)
Chúc bạn học tốt
`a, = 5^3 xx 3^3 = 15^3`
`b, = 12^3 xx 4^3 = 48^3`
`c, = 625^3 xx 8^3 = 5000^3`
`d, = 625 ^3 xx 125^3 = 78125^3`
`e, = 5^20 : 5^14 = 5^6`
1,\(125\cdot27=5^3\cdot3^3=\left(5\cdot3\right)^3=15^3\)
2, \(12^3\cdot64=12^3\cdot4^3=\left(12\cdot4\right)^3=48^3\)
3, \(25^6\cdot8^3=\left(5^2\right)^6\cdot\left(2^3\right)^3=5^8\cdot2^9\)
4, \(25^6\cdot125^3=\left(5^2\right)^3\cdot\left(5^3\right)^3=5^6\cdot5^9=5^{15}\)
5,\(625^5:25^7=\left(5^4\right)^5:\left(5^2\right)^7=5^{20}:5^{14}=5^6\)
a: \(2^6\cdot3^3=\left(2^2\cdot3\right)^3=12^3\)
b: \(6^4\cdot8^3=2^4\cdot3^4\cdot2^9=2^{13}\cdot3^4\)
c: \(16\cdot81=36^2\)
d: \(25^4\cdot2^8=100^4\)
\(a,=8\left(x^3-125\right)=8\left(x-5\right)\left(x^2+5x+25\right)\\ b,=\left(0,1+4x\right)\left(0,01-0,4x+16x^2\right)\\ c,=\left(x+\dfrac{1}{5}y\right)\left(x^2-\dfrac{1}{5}xy+\dfrac{1}{25}y^2\right)\\ d,=\left(3x-\dfrac{1}{2}y\right)\left(9x^2+\dfrac{3}{2}xy+\dfrac{1}{4}y^2\right)\\ e,=\left(x-1+3\right)\left[\left(x-1\right)^2-3\left(x-1\right)+9\right]\\ =\left(x+2\right)\left(x^2-2x+1-3x+3+9\right)\\ =\left(x+2\right)\left(x^2-5x+13\right)\\ f,=\left(\dfrac{x^2}{2}-y^2\right)\left(\dfrac{x^4}{4}+\dfrac{x^2y^2}{2}+y^4\right)\)
`a,-x^3/8 + 3/(4x^2) - 3/(2x) +1`
`=-(x^3/8 - 3/(4x^2) + 3/(2x) - 1)`
`=-(x/2 - 1)^3`
`b,x^6 - 3/(2x^{4} y) + 3/(4x^{2}y^{2}) - 1/(8y^{3})`
`=(x^3 - 1/(2y))^{3}`
