Gọi A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F(M) là trung điểm của A’B’.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 10 2017
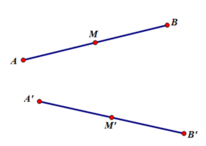
Gọi A', B', M' lần lượt là ảnh của A, B, M qua phép dời hình F
Theo tính chất 1 ⇒ AB = A'B' và AM = A'M' (1)
M là trung điểm AB ⇒ AM = 1/2 AB
Kết hợp (1) ⇒ A'M' = 1/2 A'B' ⇒ M' là trung điểm A'B'
5 tháng 8 2023
a: BE=AB/2
DF=DC/2
mà AB=DC
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
=>BEDF là hình bình hành
=>DE=BF
b: BEDF là hbh
=>BD cắt EF tại trung điểm của mỗi đường(1)
ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AC,BD,EF đồng quy
24 tháng 12 2021
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 10 2023
a/
\(ME\perp AB\) (gt)
\(AC\perp AB\Rightarrow AF\perp AB\)
=> ME//AF
\(AB\perp AC\Rightarrow AE\perp AC\)
=> MF//AE
=> AEMF là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có \(\widehat{A}=90^o\)
=> AEMF là HCN (hbh có 1 góc vuông là HCN)
b/
Ta có
MF
Xét tg vuông ABC có
MB=MC (gt); MF//AE => MF//AB
=> AF=BF (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
Ta có
MF=IF (gt)
=> AMCI là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Ta có
\(MF\perp AC\Rightarrow MI\perp AC\)
=> AMCI là hình thoi (hbh có 2 đường chéo vuông góc là hình thoi)
c/
Ta có
AI//CM (cạnh đối hình thoi) => AI//BC => ABCI là hình thang
Xét tứ giác ABMI có
AI//BC (cmt) => AI//BM
MF//AB (cmt) => MI//AB
=> ABMI là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Để ABCI là hình thang cân => AB=CI (1)
Ta có
AB=MI (cạnh đối hình bình hành ABMI) (2)
AM=CI (cạnh đối hình thoi AMCI) (3)
Từ (1) (2) (3) => AB=AM=MI=CI
Xét tg vuông ABC có
BM=CM \(\Rightarrow AM=BM=CM=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> AB=AM=BM => tg ABM là tg đều \(\Rightarrow\widehat{B}=60^o\)
Để ABCI là hình thang cân thì tg vuông ABC có \(\widehat{B}=60^o\)
d/
Xét tứ giác ADBM có
DE=ME (gt)
AE=BE (gt)
=> ADBM là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AD//BM (cạnh đối hbh) => AD//BC
Ta có
AI//CM (cạnh đối hình thoi AMCI)
=> A;D;I thẳng hàng (từ 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
Ta có
AD=BM (cạnh đối hbh ADBM)
AI=CM (cạnh đối hình thoi AMCI)
BM=CM (gt)
=> AD=AI => A là trung điểm DI
A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB
M’ = F(M) ⇒ A’M’ = kAM
M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’
Vậy M’ là trung điểm của A’B’