Hình thang ABCD (AB // CD) có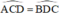 
Chứng minh rằng ABCD là hình thang cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 8 2023
Xét hình thang ABCD ta có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
mà \(\left\{{}\begin{matrix}\widehat{B}+\widehat{D}=180^o\left(đề.bài\right)\\\widehat{B}+\widehat{A}=180^o\left(t/c.hình.thang\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{C}=\widehat{D}\)
⇒ ABCD là hình thang cân (dpcm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 8 2023
Ta có : AB // CD ⇒ \(\widehat{B}\) + \(\widehat{C}\) = 180o mà \(\widehat{B}+\widehat{D}=\) 180o ⇒ \(\widehat{D}=\widehat{C}\)
Vì AB // CD; \(\widehat{D}=\widehat{C}\) vậy ABCD là hình thang cân
LC
19
30 tháng 12 2018
- Gọi O là giao điểm của AC và BD.
- AB//CD nên góc BAC = góc ACD (so le trong), tương tự góc ABD=góc BDC.
- Theo đề bài góc ACD=gócBDC nên góc BAC=góc ABD.
=>Tam giác ABO cân tại O => 0A=0B.(1)
Tương tự tam giác ODC cân tại O =>OD=OC.(2)
Lại có góc AOD=góc BOC (đối đỉnh ) (3)
Từ (1), (2), (3) suy ra tam giác AOD = tam giác OBC nên suy ra :
+ AD=BC (*)
+ Góc ADB=góc BCA(**)
Từ (*) và (**) suy ra hình thang ABCD cân(hình thang có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau )
NV
31 tháng 12 2018
- Gọi O là giao điểm của AC và BD.
- AB//CD nên góc BAC = góc ACD (so le trong), tương tự góc ABD=góc BDC.
- Theo đề bài góc ACD=gócBDC nên góc BAC=góc ABD.
=>Tam giác ABO cân tại O => 0A=0B.(1)
Tương tự tam giác ODC cân tại O =>OD=OC.(2)
Lại có góc AOD=góc BOC (đối đỉnh ) (3)
Từ (1), (2), (3) suy ra tam giác AOD = tam giác OBC nên suy ra :
+ AD=BC (*)
+ Góc ADB=góc BCA(**)
Từ (*) và (**) suy ra hình thang ABCD cân(hình thang có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau )
NN
4
24 tháng 7 2015
- Gọi O là giao điểm của AC và BD.
- AB//CD nên góc BAC = góc ACD (so le trong), tương tự góc ABD=góc BDC.
- Theo đề bài góc ACD=gócBDC nên góc BAC=góc ABD.
=>Tam giác ABO cân tại O => 0A=0B.(1)
Tương tự tam giác ODC cân tại O =>OD=OC.(2)
Lại có góc AOD=góc BOC (đối đỉnh ) (3)
Từ (1), (2), (3) suy ra tam giác AOD = tam giác OBC nên suy ra :
+ AD=BC (*)
+ Góc ADB=góc BCA(**)
Từ (*) và (**) suy ra hình thang ABCD cân(hình thang có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau )
7 tháng 8 2016
gọi BD giao với AC tại M
xét tam giác MDC ta có : góc MDC= góc MCD (gt)
=> tam giác MDC cân tại M => MC=MD
ta cũng có góc MAB= góc MBA=> tam giác MAB cân tại M
=> MA=MB
xét tam giác ADM và tam giác BCM
ta có : AM=MB (CMT)
MD=MC (CMT)
góc AMD= góc BMC (đ đ)
=> tam giác ADM = tam giác BCM
=> AD=BC
mà ABCD là hình thang
=> ABCD là hình thang cân
HT
2
16 tháng 9 2019
Gọi AC cắt BD tại O
Xét tam giác DOC có : góc ODC = góc OCD (gt)
=> tam giác DOC cân tại O
=> DO = OC (đn) (1)
AB // CD (gt)
=> góc BAO = góc OCD (slt)
góc ABO = góc ODC (slt)
mà góc OCD = góc ODC (gt)
=> góc BAO = góc ABO
=> tam giác BAO cân tại O
=> OB = OA
OA + OC = AC
OB + OD = BD và (1)
=> BD = AC ; hình thang ABCD
=> ABCD là hình thang cân (dh)
16 tháng 9 2019
Gọi E là giao điểm của AC và BD.
+ \(\widehat{C}_1=\widehat{D}_1\Rightarrow\Delta EDC\) cân tại E \(\Rightarrow ED=EC\) ( 1 )
+ AB // CD \(\Rightarrow\widehat{A}_1=\widehat{C}_1\) và \(\widehat{B}_1=\widehat{D_1}\) (Các cặp góc so le trong)
Mà \(\widehat{C}_1=\widehat{D}_1\Rightarrow\widehat{A}_1=\widehat{B_1}\)
\(\Rightarrow\Delta EAB\) cân tại E \(\Rightarrow EA=EB\) ( 2 )
Từ (1) và (2) suy ra: EA + EC = EB + ED hay AC = BD.
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
Chúc bạn học tốt !!!
28 tháng 8 2022
Câu 1:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
Suy ra: DE=CF
Bài 2:
b: Xét ΔBAD và ΔABC có
AB chung
AD=BC
BD=AC
Do đó: ΔBAD=ΔABC
Suy ra: góc EAB=góc EBA
=>ΔEAB cân tại E
=>EA=EB
2 tháng 9 2021
Bài 1:
Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
Suy ra: \(\widehat{BAC}=\widehat{ABD}\)
hay \(\widehat{EAB}=\widehat{EBA}\)
hay ΔEAB cân tại E
Gọi E là giao điểm của AC và BD.
+
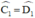⇒ ΔEDC cân tại E ⇒ ED = EC (1)
+ AB//CD ⇒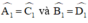
(Các cặp góc so le trong)
Mà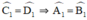
⇒ ΔEAB cân tại E ⇒ EA = EB (2)
Từ (1) và (2) suy ra: EA + EC = EB + ED hay AC = BD.
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.