Cho hai hình bình hành ABCD và ABEF không nằm cùng trong một mặt phẳng. Gọi M và N là hai điểm di động tương ứng trên AD và BE sao cho A M M D = B N N E
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 12 2019
a) Do các tứ giác ABCD và ABEF là các hình bình hành
=> O là trung điểm của AC và BD
và O’ là trung điểm của AE và BF. (tính chất hình bình hành).
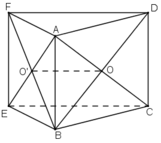
+ ΔBFD có OO’ là đường trung bình nên OO’ // DF
mà DF ⊂ (ADF)
⇒ OO' // (ADF)
+ ΔAEC có OO’ là đường trung bình nên OO’ // EC
mà EC ⊂ (BCE)
⇒ OO’ // (BCE).
b)
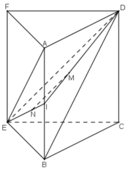
Ta thấy mp(CEF) chính là mp(CEFD).
Gọi I là trung điểm của AB:
+ M là trọng tâm ΔABD
⇒ IM/ ID = 1/3.
+ N là trọng tâm ΔABE
⇒ IN/IE = 1/3.
+ ΔIDE có IM/ID = IN/IE = 1/3
⇒ MN // DE mà ED ⊂ (CEFD)
nên MN // (CEFD) hay MN // (CEF).
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
a) Ta có: AD // BC (ABCD là hình bình hành)
Mà AD thuộc (AFD), BC thuộc (BEC)
Nên (AFD) // (BEC)
b) Trong (ABEF) kẻ đường thẳng d qua M // AF
Ta có: d cắt AB tại I, d cắt EF tại J (1)
Trong (ABCD) có I thuộc (P) mà (P) // (AFD)
Suy ra từ I kẻ IH // AD (2)
(1)(2) suy ra (IJH) trùng (P) và // (AFD)
Ta có: (P) cắt AC tại N mà AC thuộc (ABCD), IH thuộc (P) và (ABCD)
Suy ra: IH cắt AC tại N
Ta có các hình bình hành IBCH, IBEJ
Gọi O là trung điểm của AB
Có M là trọng tâm △ABE
Suy ra: \(\dfrac{MO}{ME}=\dfrac{1}{2}\).
Ta có: AB // CD suy ra: AI // CH
Định lí Ta-lét: \(\dfrac{AN}{NC}=\dfrac{AI}{CH}\)
mà CH = IB (IBCH là hình bình hành)
Suy ra: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}\)
Ta có: AB // EF nên OI // EJ
Do đó: \(\dfrac{OI}{EJ}=\dfrac{MO}{ME}=\dfrac{1}{2}\)
Mà EJ = IB (IBEJ là hình bình hành)
Suy ra: \(\dfrac{OI}{IB}=\dfrac{1}{2}\) hay IB = 2OI
Ta có: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}=\dfrac{AO+OI}{2OI}\)
Mà OA = OB (O là trung điểm AB)
Nên \(\dfrac{AN}{NC}=2\).
Q
31 tháng 3 2017
a) OO' là đường trung bình của tam giác DBF nên OO' // DF.
DF nằm trong mặt phẳng (ADF) nên OO' // mp(ADF).
Tương tự OO' // CE mà CE nằm trong mặt phẳng (BCE) nên OO' // mp(BCE).
b) Gọi J là trung điểm đoạn thẳng AB, theo định lí Ta-lét \(\Rightarrow\) MN // DE => đpcm.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
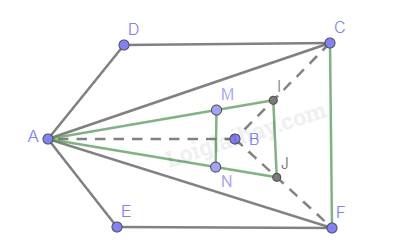
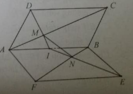
Gọi I,J lần lượt là trung điểm của BC, BF
Suy ra, IJ là đường trung bình của tam giác BCF.
Do đó, IJ // CF (1)
Tam giác AIJ có: \(\frac{{AM}}{{AI}} =\frac{{AN}}{{AJ}}= \frac{2}{3}\)
Suy ra, MN // IJ (theo Ta lét) (2)
Từ (1) và (2) suy ra MN // CF, mà CF nằm trong (ACF).
Suy ra MN // (ACF)
CM
17 tháng 9 2017
MN // DE nên DM, NE cắt nhau tại điểm I và
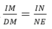
Lại có
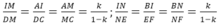
Mặt khác:
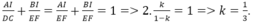
Đáp án A.
CM
7 tháng 8 2019
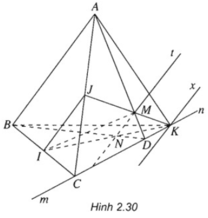
a)
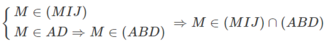
Ta cũng có:
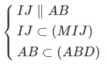
⇒ (MIJ) ∩ (ABD) = d = Mt và Mt // AB // IJ
b) Ta có: Mt // AB ⇒ Mt ∩ BD = N
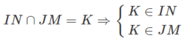
Vì K ∈ IN ⇒ K ∈ (BCD)
Và K ∈ JM ⇒ K ∈ (ACD)
Mặt khác (BCD) ∩ (ACD) = CD do đó K ∈ CD. Do vậy K nằm trên hai nửa đường thẳng Cm và Dn thuộc đường thẳng CD. ( Để ý rằng nếu M là trung điểm của AD thì sẽ không có điểm K.)
c) Ta có:
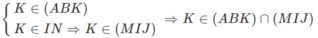
Mà
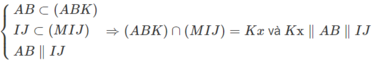
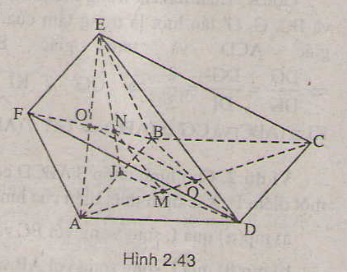
Trong mặt phẳng (ADF), kẻ đường thẳng MP // DF (P ∈ AF)
Ta có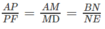
Nên PN // FE. Do đó (MNP) // (DEF).
Vậy MN song song với mặt phẳng (DEF) cố định.