Tại sao muốn giảm r, lại phải tăng tiết diện dây và tăng khối lượng đồng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 11 2021
\(\dfrac{R_1}{R_2}=\dfrac{\rho\dfrac{l_1}{S_1}}{\rho\dfrac{l_2}{S_2}}=\dfrac{l_1}{S_1}.\dfrac{S_2}{l_2}=\dfrac{l_1}{S_1}.\dfrac{\dfrac{1}{2}S_1}{3l_1}=\dfrac{1}{6}\Rightarrow R_2=6R_1\)
Vậy điện trở của dây tăng gấp 6 lần
22 tháng 5 2021
- Nhiệt tăng -> vật nở ra -> thể tích của vật tăng
Vì công thức tính khối lượng riêng của chất là \(D=\dfrac{m}{V}\) nên D và V tỉ lệ nghịch với nhau, nghĩa là V càng tăng thì D càng giảm, nên nhiệt tăng thì khối lượng riêng giảm nhé, không có chuyện chất bị mất bớt đâu :))
- Tương tự đối với nhiệt giảm: Nhiệt giảm -> vật co lại -> V giảm -> D tăng (D và V tỉ lệ nghịch với nhau, nghĩa là V càng giảm thì D càng tăng).
Thắc mắc gì bạn hỏi dưới phần bình luận nhé!
N
13 tháng 11 2021
Lập luận nào dưới đây là đúng? Điện trở của dây dẫn:
A. tăng lên gấp đôi khi chiều dài tăng lên gấp đôi và tiết diện dây tăng lên gấp đôi.
B. giảm đi một nửa khi chiều dài tăng lên gấp đôi và tiết diện dây tăng lên gấp đôi.
C. giảm đi một nửa khi chiều dài tăng lên gấp đôi và tiết diện dây tăng lên gấp bốn.
D. tăng lên gấp đôi khi chiều dài tăng lên gấp đôi và tiết diện dây giảm đi một nửa.
22 tháng 12 2020
Theo đề bài, ta có: \(\left\{{}\begin{matrix}\rho=\rho'\\l=l'\\S'=2S\\R=?\end{matrix}\right.\)
Từ công thức \(R=\rho.\dfrac{l}{S}\rightarrow\rho=\dfrac{R.S}{l}\)
\(\rho=\rho'\\ \rightarrow\dfrac{R.S}{l}=\dfrac{R'.S'}{l}\\ \rightarrow R.S=R'.S'\\ \rightarrow R.S=R'.2S'\\ \rightarrow R=2.R'\\ \rightarrow R'=\dfrac{R}{2}\)
Vậy điện trở giảm 1 nửa
\(\rightarrow D\) Giảm đi 2 lần
Ta có: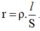
Vậy nếu muốn giảm r thì phải tăng tiết diện S lên.
Mà khối lượng dây: m = D.V = D.l.S nên khối lượng dây đồng tăng lên điều này tốn kém không phù hợp trong việc truyền tải điện năng.