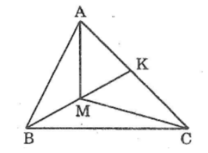
Cho tam giác ABC, điểm M nằm trong tam giác đó. Tia BM cắt AC ở K. So sánh ∠(AMC) và ∠(ABC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 8 2017
a) Góc AMK là góc ngoài của tam giác ABM => ^AMK=^BAM+^ABM
hay ^AMK=^BAM+^ABK => ^AMK>^ABK. (1)
b) Tương tự: ^CMK là góc ngoài tam giác BMC => ^CMK>CBM hay ^CMK>CBK (2)
Từ (1) và (2) => ^AMK+CMK>^ABK+^CBK => ^AMC>^ABC.
!
KT
31 tháng 7 2018
a) Góc AMK là góc ngoài tam giác AMB tại đỉnh M
=> góc AMK = góc ABK + góc BAM
=> góc AMK > góc ABK (1)
b) góc CMK là góc ngoài tam giác CMB tại đỉnh M
=> góc CMK = góc CBK + góc MCB
=> góc CMK > góc CBK (2)
Lấy (1) + (2) theo vế ta được:
góc AMK + góc CMK > góc ABK + góc CBK
=> góc AMC > góc ABC
24 tháng 10 2015
a) Góc AMK là góc ngoài của tam giác ABM tại đỉnh M => góc AMK > góc ABM hay góc AMK > góc ABK
b) góc CMK là góc ngoài của tam giác AMC tại đỉnh M => góc CMK > góc CBM Hay góc CMK > góc CBK
=> góc AMK + góc CMK > góc ABK + góc CBK
=> góc AMC > góc ABC
CM
27 tháng 4 2019
Trong ΔAMB ta có góc AMK là góc ngoài tại đỉnh M.
⇒ ∠(AMK) > ∠(ABK) (tính chất góc ngoài tam giác) (1)
5 tháng 8 2019
Câu hỏi của ICHIGO HOSHIMIYA - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé! Nhớ thay điểm D bằng điểm K
Trong ΔCBM ta có góc KMC là góc ngoài tại đỉnh M
⇒∠(KMC) > ∠(MBC) (tính chất góc ngoài tam giác) (2)
Cộng từng vế (1) và (2) ta có: ∠(AMK) +∠(KMC) > ∠(ABM) +∠(MBC)
Suy ra: ∠(AMC) > ∠(ABC)