Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Góc AMK là góc ở đỉnh M của tam giác ABM
=> góc AMK > góc ABK
b) Góc KMC là góc ngoài tại đỉnh M của tam giác CBM
=> góc KMC > góc CBK
=> góc AMK + góc KMC > góc ABK + góc CBK
nên góc AMC > góc ABC
P/s : tự vẽ hình nha

Bài 1:
a: XétΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD
b: Xét ΔDBC và ΔECB có
DB=EC
BC chung
DC=EB
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{KDB}=\widehat{KEC}\)
Xét ΔKDB và ΔKEC có
\(\widehat{KDB}=\widehat{KEC}\)
BD=CE
\(\widehat{KBD}=\widehat{KCE}\)
Do đó: ΔKDB=ΔKEC

cho t.giác ABC vuông ở C, có \(\widehat{C}\)=60 độ là sao vậy bn,đã vuông thì pk = 90 độ chứ

A B C M N O
Bài này mình thấy chứng minh phần b trước thì ra phần a luôn =)))
b)Tam giác ABC có 2 góc bằng nhau: \(\widehat{ABC}=\widehat{ACB}\) =>Tam giác ABC cân tại A => AB=AC (1)
Tia BM là tia phân giác của góc ABC => \(\widehat{ABM}=\widehat{BM}C=\frac{1}{2}.\widehat{ABC}\)
Tia CN là tia phân giác của góc ACB => \(\widehat{ACN}=\widehat{NCB}=\frac{1}{2}.\widehat{ACB}\)
Mà \(\widehat{ABC}=\widehat{ACB}\) <=> \(\frac{1}{2}.\widehat{ABC}=\frac{1}{2}.\widehat{ACB}\) => \(\widehat{ABM}\)\(=\widehat{ACN}\) (2)
Xét \(\Delta ABM\) và \(\Delta ACN\) có:
- \(\widehat{BAC}\) là góc chung
- AB=AC (suy ra ở (1))
- \(\widehat{ABM}\)\(=\widehat{ACN}\) (suy ra ở (2))

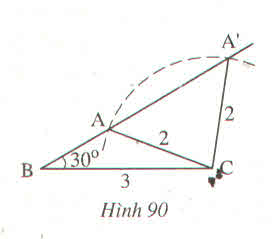
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.

a, xét △ AMB và △ AMC có:
AB=AC(gt)
góc BAM=góc CAM (gt)
AM chung
=> △ AMB= △ AMC(c.g.c)
b,xét △ AHM và △ AKM có:
AM cạnh chung
góc HAM=ˆgóc KAM (gt)
=>△ AHM= △ AKM(CH-GN)
=> AH=AK
c,gọi I là giao điểm của AM và HK
xét △ AIH và △ AIK có:
AH=AK(theo câu b)
góc AIH=ˆgóc AIK (gt)
AI chung
=> △ AIH=△ AIK (c.g.c)
=> góc AIH=ˆgóc AIK
mà góc AIH+góc AIK=180độ(2 góc kề bù)
=> HK ⊥ AM
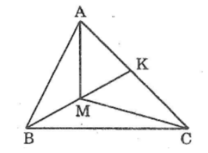

Trong ΔCBM ta có góc KMC là góc ngoài tại đỉnh M
⇒∠(KMC) > ∠(MBC) (tính chất góc ngoài tam giác) (2)
Cộng từng vế (1) và (2) ta có: ∠(AMK) +∠(KMC) > ∠(ABM) +∠(MBC)
Suy ra: ∠(AMC) > ∠(ABC)