Cho góc xOy, trên Ox lấy điểm A sao cho OA = 4cm, trên Oy lấy các điểm B và C sao cho OB = 2cm, OC = 8cm. Chứng minh rằng Δ A O B ∽ Δ C O A .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
20 tháng 3 2019
Đúng(0)
Những câu hỏi liên quan
7 tháng 3 2022
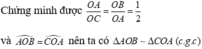
Xét ΔAOD và ΔBOC có
OA/OB=OD/OC
góc AOD chung
Do đó: ΔAOD\(\sim\)ΔBOC
DB
24 tháng 12 2022
a) Chứng minh: AD = BC.
Xét ∆OAD và ∆OBC có:
OA = OB (gt);
ˆAODAOD^ chung;
OD = OC (gt)
Do đó ∆OAD = ∆OBC (c.g.c)
Suy ra AD = BC (hai cạnh tương ứng)
b) Chứng minh: ∆EAC = ∆EBD.
Vì ∆OAD = ∆OBC (câu a)
Nên ˆA2=ˆB2A^2=B^2 (hai góc tương ứng)
Mà ˆA1+ˆA2=180oA^1+A^2=180o, ˆB1+ˆB2=180oB^1+B^2=180o (kề bù)
Do đó ˆA1=ˆB1A^1=B^1.
Mặt khác, OA = OB, OC = OD
Suy ra OC – OA = OD – OB
Do đó AC = BD
Xét ∆EAC và ∆EBD có:
ˆA1=ˆB1A^1=B^1 (cmt);
AC = BD (cmt);
ˆOCB=ˆODAOCB^=ODA^ (vì ∆OAD = ∆OBC)
Do đó ∆EAC = ∆EBD (g.c.g).
c) Chứng minh: OE là tia phân giác của góc xOy.
Vì ∆EAC = ∆EBD (câu b)
Nên AE = BE (hai cạnh tương ứng).
Xét ∆OAE và ∆OBE có:
OA = OB (gt);
Cạnh OE chung;
AE = BE (cmt)
Do đó ∆OAE và ∆OBE (c.c.c)
Suy ra ˆAOE=ˆBOEAOE^=BOE^ (hai góc tương ứng)
Hay OE là phân giác của góc xOy.
24 tháng 6 2023
a: Xét ΔOAB và ΔOCD có
OA/OC=OB/OD
góc O chung
=>ΔOAB đồng dạng với ΔOCD
b: Xét ΔMDA và ΔMBC có
góc MAD=góc MCB
góc DMA=góc BMC
=>ΔMDA đồng dạng với ΔMBC
=>MD/MB=MA/MC
=>MD*MC=MB*MA
c: ΔOAB đồng dạng với ΔOCD
=>OA/OC=OB/OD=AB/CD=C OAB/ C OCD
=>C OAB/C OCD=OA/OC=8/6=4/3
=>C OAB/4=C OCD/3=38,5/7=5,5
=>C OAB=22; C OCD=16,5
=>AB+OA+OB=22 và CD+OC+OD=16,5
=>AB=22-8-4=10cm và CD=16,5-6-3=16,5-9=7,5cm
7 tháng 3 2021
Bổ sung ĐK : ^xOy \(\ne\)1800
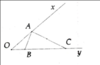
Xét tam giác AOB và tam giác COA ta có :
O _ chung
\(\frac{OA}{OC}=\frac{OB}{OA}=\frac{4}{8}=\frac{2}{4}=\frac{1}{2}\)
Vậy tam giác AOB ~ tam giác COA ( c.g.c )
10 tháng 4 2020
a.OC=OA+AC
OD=OB+BD
mà OA=OB(gt);AC=BD(gt)
=>OC=OD
Xét tam giác OAD và tam giác OBC có:OA=OB(gt)
góc O chung
OD=OC(cmt)
=>tam giác OAD=tam giác OBC(c.g.c)=>AD=BC(hai cạnh tương ứng)(đpcm)
b.tam giác OAD=tam giác OBC(câu a)=>góc OAD=góc OBC(hai góc tương ứng)
góc ODA=góc OCB(hai góc tương ứng) hay góc BDE=góc ACE
góc OAD+góc DAC=180 độ (hai góc kề bù)
góc OBC+góc CBD=180 độ (hai góc kề bù)
=>góc DAC=góc CBD hay góc EAC=góc EBD
Xét tam giác EAC và tam giác EBD có:
Góc ACE=góc BDE(cmt)
AC=BD(gt)
góc EAC=góc EBD(cmt)
=>tam giác EAC=tam giác EBD(g.c.g)(đpcm)
c.tam giác EAC=tam giác EBD(câu b)=>EC=ED(hai cạnh tương ứng)
Xét tam giác OEC và tam giác OED có:
OC=OD(câu a)
EC=ED(cmt)
OE chung
=>tam giác OEC=tam giác OED(c.c.c)
=>góc EOC=góc EOD(hai góc tương ứng)=>OE là phân giác góc COD hay OE là phân giác góc xOy (đpcm)
7 tháng 1 2022
a: Xét ΔOAH và ΔOBH có
OA=OB
\(\widehat{AOH}=\widehat{BOH}\)
OH chung
Do đó: ΔOAH=ΔOBH
b: Xét tứ giác AOBM có
H là trung điểm của AB
H là trung điểm của OM
Do đó: AOBM là hình bình hành
Suy ra: MB//OA