Trong ví dụ 4, hãy tính các cạnh OP, OQ qua côsin của các góc P và Q.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Định lí:
Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau: a2 = b2 + c2 - 2bc.cosA (1)
b2 = a2 + c2 - 2bc.cosB (2)
c2 = a2 + b2 - 2bc.cosC (3)
Hệ quả: Từ định lí cosin suy ra:
cosA = cosB =
cosC =

Ta có hình vẽ:
a) Vì \(OP\perp OM\Rightarrow POM=90^o;OQ\perp ON\Rightarrow QON=90^o\)
Ta có: MOP + PON = MON
=> 90o + PON = 140o
=> PON = 140o - 90o = 50o (1)
Lại có: MOQ + QON = MON
=> MOQ + 90o = 140o
=> MOQ = 140o - 90o = 50o (2)
Từ (1) và (2) => PON = MOQ = 50o
b) Ta có: POQ + PON = QON
=> POQ + 50o = 90o
=> POQ = 90o - 50o = 40o
Giải:
Ta có: \(\widehat{MOQ}+\widehat{NOQ}=\widehat{MON}\)
\(\Rightarrow\widehat{MOQ}+90^o=140^o\) ( vì OQ _|_ ON nên \(\widehat{NOQ}=90^o\) )
\(\Rightarrow\widehat{MOQ}=50^o\)
\(\widehat{MOP}+\widehat{NOP}=\widehat{MON}\)
\(\Rightarrow90^o+\widehat{NOP}=140^o\) ( vì OP _|_ OM nên \(\widehat{MOP}=90^o\) )
\(\Rightarrow\widehat{NOP}=50^o\)
\(\Rightarrow\widehat{MOQ}=\widehat{NOP}=50^o\)
b) Ta có: \(\widehat{MOQ}+\widehat{POQ}+\widehat{NOP}=\widehat{MON}\)
\(\Rightarrow50^o+\widehat{POQ}+50^o=120^o\)
\(\Rightarrow\widehat{POQ}=20^o\)

Bạn tự vẽ hình nha![]()
a.
MOQ + QON = MON
MOQ + 900 = 1400
MOQ = 1400 - 900
MOQ = 500
NOP + POM = MON
NOP + 900 = 1400
NOP = 1400 - 900
NOP = 500
mà MOQ = 500
=> NOP = MOQ
b.
MOQ + QOP + PON = MON
500 + QOP + 500 = 1400
QOP = 1400 - 500 - 500
QOP = 400
Chúc bạn học tốt![]()
a)Vì OP vuông góc với OM, OQ vuông góc với ON
Suy ra:MOP=QON=900
Mà MOQ+POQ=900(1)
NOP+POQ=900(2)
Từ (1) và (2) suy ra MOQ=NOP
b) Vì MON=MOP+PON
Thay số:1400=900+PON
PON=1400-900=500
Mà PON=MOQ
Tacó:MON=MOQ+PON+QOP
Thay số:1400=500+500+POQ
POQ=400

a, Do OP vuông góc với OM=> góc mOp = 90^0
Do OQ vuông góc với ON => góc nOq = 90^0
=> góc mOp = góc nOq
b,Ta có nOp = góc mOn - góc mOp = 140^0 - 90^0 = 30^0
Vậy góc pOq = góc nOq - góc nOp = 90^0 -30^0 = 60^0
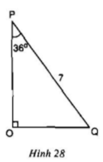
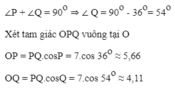
Ta có: ∠P + ∠Q = 90o ⇒ ∠ Q = 90o - 36o= 54o
Xét tam giác OPQ vuông tại O
OP = PQ.cosP = 7.cos 36o ≈ 5,66
OQ = PQ.cosQ = 7.cos 54o ≈ 4,11