Cho Δ A B C = Δ M N P , trong đó A ^ = 30 o , P ^ = 60 o . So sánh các góc N

PT

Pham Trong Bach

26 tháng 12 2017

Cho Δ A B C = Δ M N P , trong đó A ^ = 30 o , P ^ = 60 o . So sánh các góc N; M; P A. N ^ = P ^ > M ^ B. N ^ > P ^ = M ^ C. N ^ > P ^ > M ^ D. N ^ < P ^ < M ^ ...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

26 tháng 12 2017

Đúng(0)

T

ToanTungTang

13 tháng 3 2021

Cho góc xOy, trên Ox lấy các điểm M và P, trên Oy lấy các điểm N và Q. Chứng minh rằng Δ O M N ∽ Δ O P Q nếu biết một trong các trường hợp sau:

a) O M = 2 c m ; O N = 1 , 5 c m ; O P = 4 c m ; O Q = 3 c m ;

b) M là trung điểm của OP, N là trung điểm của OQ

#Toán lớp 8

0

PT

Pham Trong Bach

6 tháng 12 2017

Trong các mệnh đề sau đây mệnh đề nào là đúng?a) Đường thẳng Δ là đường vuông góc chung của hai đường thẳng a và b nếu Δ ⊥a và Δ ⊥b.b) Gọi (P) là mặt phẳng song song với cả hai đường thẳng a và b chéo nhau thì đường vuông góc chung của a và b luôn luôn vuông góc với (P).c) Gọi Δ là đường vuông góc chung của hai đường thẳng chéo nhau a và b thì Δ là giao tuyến của hai mặt phẳng (a,...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

6 tháng 12 2017

a) Sai

Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"

b) Đúng

c) Đúng

d) Sai

Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.

e) Sai.

Đúng(0)

CT

chế trần ngọc thinh

14 tháng 7 2019 - olm

Cho tam giác ABC có ba góc nhọn, các điểm M, N thứ tự là trung điểm của BC và AC. Các đường trung trực của BC và AC cắt nhau tại O. Qua A kẻ đường thẳng song song với OM, qua B kẻ đường thẳng song song với ON, chúng cắt nhau tại Ha) Nối MN, Δ AHB đồng dạng với tam giác nào?b) Gọi G là trọng tâm Δ ABC, chứng minh Δ AHG đồng dạng với Δ MOG?c) Chứng minh ba điiểm M, O, G thẳng...

Đọc tiếp

#Toán lớp 8

0

MV

Minh Vương Nguyễn Bá

20 tháng 4 2022

Cho Δ ABC vuông tại A, có góc ABC = 60°. Tia phân giác của góc B cắt AC tại E. Từ E vẽ EH ⊥ BC (H ∈ BC). a) Chứng minh Δ ABE = Δ HBE. b) Qua H vẽ HK // BE (K ∈ AC). Chứng minh Δ EHK đều. c) HE cắt BA tại M, MC cắt BE tại N. Chứng minh NM=NC

#Toán lớp 7

1

KP

Khanh Pham

20 tháng 4 2022

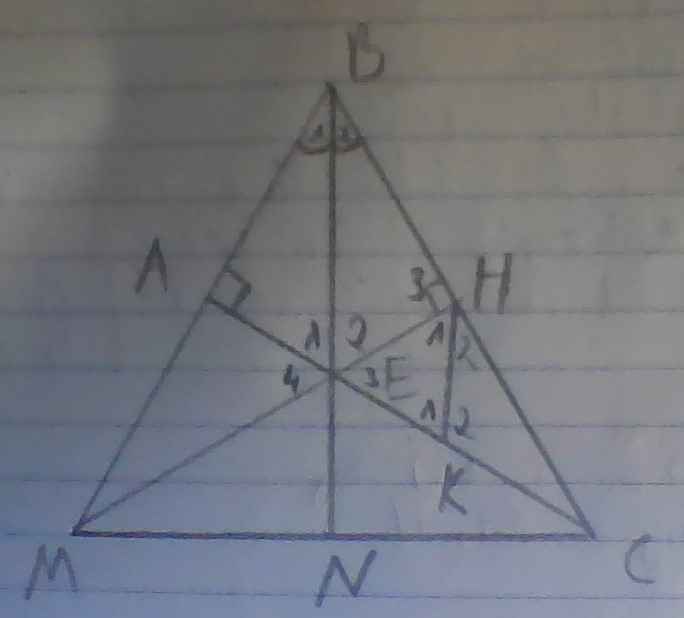
undefined

a) có BE là tia p/g của góc ABC

=> góc B₁ = góc B₂ = góc ABC/2 = 60⁰ /2 = 30⁰

có △ABC vuông tại A => △ABE vuông tại A

EH⊥BC=> △HBE vuông tại H

Xét △ vuông ABE và △vuông HBE có

góc B₁ = góc B₂

BE chung

=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)

b) có △ABE vuông tại A=> góc B₁ + góc E₁ = 90⁰

góc E₁ = 60⁰ ( vì góc B₁ = 30⁰)

có △ vuông ABE =△vuông HBE

=> góc E₁ = góc E₂

mà HK//BE => góc E₁ = góc K₁ (ĐV)

và góc E₂ = góc H₁ (SLT)

=> góc E₁ = góc E₂ = góc K₁=góc H₁ = 60⁰

=> △HEK đều

c) có góc E₁ = góc E₂ ; góc E₃ = góc E₄

=>góc E₁ +góc E₄ = góc E₂ + góc E₃

=> góc BEM= góc BEC

Xét △BEM và △ BEC có

góc B₁ = góc B₂

BE chung

góc BEM= góc BEC

=> △BEM = △ BEC (g.c.g)

=>BM=BC

=>△BMC cân tại B

trong △BMC có BN là đường p/g xuất phát từ đỉnh B

lại có △BMC cân tại B

=> BN cũng là đường trung tuyến xuất phát từ đỉnh B

=> N là trung điểm của MC

=> NM=NC

Đúng(0)

PT

Pham Trong Bach

2 tháng 10 2019

Cho Δ A B C = Δ M N P trong đó A ^ = 30 ° ; P ^ = 60 ° . So sánh các góc N ^ ; M ^ ; P ^ A. M ^ > P ^ > N ^ B. M ^ = P ^ < N ^ C. M ^ < P ^ < N ^ D. M ^ < P ^ ...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

2 tháng 10 2019

Đáp án C

Đúng(0)

KN

khải nguyên gia tộc

25 tháng 4 2016 - olm

Cho tam giác ABC cân tại A (góc A<90 độ) các đường cao BD và CE ( D∈AC; E∈AB ) cắt nhau tại H

a. Chứng minh Δ ABD= Δ ACE

b. Chứng minh Δ BHC là tam giác cân

c. So sánh HB và HD

d. Trên tia đối EH lấy điểm N sao cho NH<HC; Trên tia đối của tia DH lấy điểm M sao cho MH=NH. Chứng minh các đường thẳng BN;AH;CM đồng quy

#Toán lớp 7

3

KN

khải nguyên gia tộc

25 tháng 4 2016

a. Xét ΔABD và ΔBCE có: ∠ ADB = ∠ AEC = 90º (gt)

BA = AC (gt)

∠BAC chung

⇒ ΔABD = ΔACE (cạnh huyền – góc nhọn)

b). ΔABD = ΔACE ⇒ ∠ABD = ∠ACE (hai góc tương ứng)

mặt khác: ∠ABC = ∠ACB (ΔABC cân tại A )

⇒ ∠ABC – ∠ABD = ∠ACB – ∠ACE => ∠HBC = ∠HCB

⇒ ΔBHC là tam giác cân

c. ΔHDC vuông tại D nên HD <HC

mà HB = HC (ΔAIB cân tại H)

=> HD < HB

d. Gọi I là giao điểm của BN và CM

Xét Δ BNH và Δ CMH có:

BH = CH (Δ BHC cân tại H)

∠ BHN = CHM(đối đỉnh)

NH = HM (gt)

=> Δ BNH = Δ CMH (c.g.c) ⇒ ∠HBN = ∠ HCM

Lại có: ∠ HBC = ∠ HCB (Chứng minh câu b)

⇒ ∠HBC + ∠HBN = ∠HCB + ∠HCM => ∠IBC = ∠ICB

⇒ IBC cân tại I ⇒ IB = IC (1)

Mặt khác ta có: AB = AC (Δ ABC cân tại A) (2)

HB = HC (Δ HBC cân tại H) (3)

Từ (1); (2) và (3) => 3 điểm I; A; H cùng nằm trên đường trung trực của BC

=> I; A; H thẳng hàng => các đường thẳng BN; AH; CM đồng quy

Đúng(1)

JJ

Jav Jav Jav

17 tháng 4 2017

Ê mày bị điên ak mà tự làm tự trả lời

Đúng(0)

TD

Thùy Dương Nguyễn

17 tháng 2 2022

cho Δ MNP ( góc M = 90 ). Qua M kẻ đt d//Np . Từ N kẻ NS vuông góc d. Từ P kẻ PK vuông góc d a) Δ NPKS là hình gì ?b) Gọi O là giao điểm của Nk và SP Cm: Sn.Op = So.Kpc) Gọi A là giao điểm của Mn và Sp Tính S Δ NAP biết MN = 3cm , Np = 5...

Đọc tiếp

#Toán lớp 8

0

HT

Hoàng Thị Thanh Thảo

24 tháng 10 2016

Cho Δ ABC có góc C = 30^o. Gọi số đo các góc A, B lần lượt là x, y. Tính x và y trong mỗi trường hợp sau:

a) x = 2y

b) x - y = 10^o

c^*) 3x = 2y

#Toán lớp 7

1

NH

Nguyễn Huy Tú

24 tháng 10 2016

Giải:

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\Rightarrow\widehat{A}+\widehat{B}+30^o=180^o\)

\(\Rightarrow\widehat{A}+\widehat{B}=150^o\)

a) Ta có: \(\widehat{A}+\widehat{B}=150^o\)

\(\Rightarrow x+y=150^o\)

Mà x = 2y

\(\Rightarrow2y+y=150^o\)

\(\Rightarrow3y=150^o\)

\(\Rightarrow y=50^o\)

\(\Rightarrow x=50^o.2=100^o\)

Vậy \(y=50^o,x=100^o\)

b) Ta có: \(\widehat{A}+\widehat{B}=150^o\)

\(\Rightarrow x+y=150^o\)

Mà \(x-y=10^o\)

\(\Rightarrow x=\left(150^o+10^o\right):2=80^o\)

\(\Rightarrow y=150^o-80^o=70^o\)

Vậy \(x=80^o,y=70^o\)

c) Ta có: \(3x=2y\Rightarrow\frac{x}{3}=\frac{y}{2}\) và \(\widehat{A}+\widehat{B}=150^o\) hay \(x+y=150^o\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{2}=\frac{x+y}{3+2}=\frac{150^o}{5}=30^o\)

+) \(\frac{x}{3}=30^o\Rightarrow x=90^o\)

+) \(\frac{y}{2}=30^o\Rightarrow y=60^o\)

Vậy \(x=90^o,y=60^o\)

Đúng(0)

DA

dương anh khoa

7 tháng 3 2022

Cho góc xOy, trên Ox lấy các điểm A và C, trên Oy lấy các điểm B và D. Chứng minh rằng Δ A O D ∽ Δ B O C nếu OA = 4cm, OC = 15cm, OB = 6cm, OD =10cm.

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

7 tháng 3 2022

Xét ΔAOD và ΔBOC có

OA/OB=OD/OC

góc AOD chung

Do đó: ΔAOD\(\sim\)ΔBOC

Đúng(1)

HA

Hinamori Amu

22 tháng 10 2016

Câu hỏi hay

Cho Δ ABC vẽ tia phân giác AD của góc A biết góc ADB = 80^o; góc B = \(\frac{3}{2}\) góc C. Tính các góc của Δ ABC.

#Toán lớp 7

2

SG

soyeon_Tiểubàng giải

22 tháng 10 2016

Ta có hình vẽ:

Ta có: ADC + ADB = 180^o (kề bù)

=> ADC + 80^o = 180^o

=> ADC = 180^o - 80^o = 100^o

Vì AD là phân giác của góc A nên \(CAD=DAB=\frac{CAB}{2}\)

Xét Δ ACD có: CAD + ADC + ACD = 180^o

=> \(\frac{CAB}{2}\) + 100^o + ACD = 180^o

=> \(\frac{CAB}{2}\) + ACD = 180^o - 100^o = 80^o (1)

Xét Δ ADB có: ADB + DAB + ABD = 180^o

=> 80^o + \(\frac{CAB}{2}\) + ABC = 180^o

=> \(\frac{CAB}{2}\) + ABC = 180^o - 80^o = 100^o (2)

Từ (1) và (2) \(\Rightarrow\left(\frac{CAB}{2}+ABC\right)-\left(\frac{CAB}{2}+ACD\right)=100^o-80^o\)

=> ABC - ACD = 20^o

=> \(\frac{3}{2}ACD-ACD=20^o\)

\(\Rightarrow\frac{1}{2}ACD=20^o\Rightarrow ACD=20^o:\frac{1}{2}=40^o\)

=> ABC = 20^o + 40^o = 60^o

Lại có: ABC + ACD + CAB = 180^o

=> 60^o + 40^o + CAB = 180^o

=> 100^o + CAB = 180^o

=> CAB = 180^o - 100^o = 80^o

Vậy CAB = 80^o; ABC = 60^o; ACB = ACD = 40^o

Đúng(0)

KL

khánh linh cute

27 tháng 7 2017

bạn làm đúng rồi đó

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP