B. Phần tự luận (6 điểm)
Cho tam giác ABC có AB < AC, tia phân giác của góc A cắt BC tại D. Trên cạnh AC lấy điểm E sao cho AB=AE
a. Chứng minh ΔADE = ΔADB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 3 2022
a: XétΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó:ΔABD=ΔAED
Suy ra: BD=ED
b: ta có: BD=ED
mà ED<DC
nên BD<DC
NB
3 tháng 5 2023
a)xét tg ABD và tg CBD có:
+ AB=BE(gt)
+ góc ABD = EBD (BD là phân giác)
+BD chung
=>tg ABD= tg EBD(c.gc)
b) vì tg ABD=tgEBD
=> AD=DE và góc BAD = BED (=90 độ)
=> DE ⊥ BC
=> tg DEC có DC là cạnh huyền =>DC>ED mà ED=AD => DC>AD
c)xét tg BFE và tg BCA có:
+ Góc E = A (=90 độ)
+góc B chung
+ BE=BA
=>tg BFE =tg BCA (gcg)
=>BF=BC
=> tg BFC cân tại B
vì S là td FC
=>BS vừa là trung tuyến vừa là đường cao
=>BS⊥FC (1)
tg BFC có: D là giao của 2 đg cao CA và FE
=> D là trực tâm => BD ⊥ FC (2)
từ 1 và 2 => B,D,S thẳng hàng
KV
3 tháng 5 2023
Sửa đề: AB = BE (không phải AB = AE)
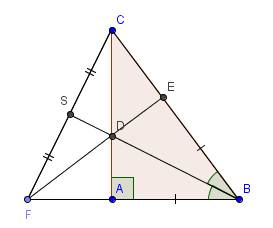
Gởi hình vẽ trước, đi công việc, tí sửa sau
17 tháng 6 2023
a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
b: DA=DM
=>góc DAM=góc DMA
16 tháng 12 2022
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE
b: Xét ΔDBF và ΔDEC có
góc DBF=góc DEC
DB=DE
góc BDF=góc EDC
Do đo: ΔDBF=ΔDEC
c:ΔDBF=ΔDEC
nên góc BDF=góc EDC
=>góc BDF+góc BDE=180 độ
=>E,D,F thẳng hàng
23 tháng 1 2022
a) Xét tam giác ABD: AB = AD (gt).
=> Tam giác ABD cân tại A.
Mà AH là phân giác góc BAD (gt).
=> AH là trung tuyến (Tính chất tam giác cân).
=> H là trung điểm của cạnh BD (đpcm).
23 tháng 1 2022
a: Ta có: ΔABD cân tại A
mà AH là đường phân giác
nên H là trung điểm của BD
b: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
Suy ra: FB=FD
Xét ΔBFE và ΔDFC có
FB=FD
\(\widehat{FBE}=\widehat{FDC}\)
BE=DC
Do đó: ΔBFE=ΔDFC
Suy ra: \(\widehat{BFE}=\widehat{DFC}\)
mà \(\widehat{DFC}+\widehat{DFB}=180^0\)
nên \(\widehat{BFE}+\widehat{BFD}=180^0\)
=>D,E,F thẳng hàng
23 tháng 1 2022
a: Ta có: ΔABD cân tại A
mà AH là đường phân giác
nên H là trung điểm của BD
b: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
Suy ra: FB=FD
Xét ΔBFE và ΔDFC có
FB=FD
\(\widehat{FBE}=\widehat{FDC}\)
BE=DC
Do đó: ΔBFE=ΔDFC
Suy ra: \(\widehat{BFE}=\widehat{DFC}\)
mà \(\widehat{DFC}+\widehat{DFB}=180^0\)
nên \(\widehat{BFE}+\widehat{BFD}=180^0\)
=>D,E,F thẳng hàng
27 tháng 8 2022
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
Suy ra: DB=DE
b: Xét ΔDBH và ΔDEC có
góc DBH=góc DEC
DB=DE
góc BDH=góc EDC
Do đó: ΔDBH=ΔDEC
c: Ta có: ΔDBH=ΔDEC
nên góc DHB=góc DCE
d: Ta có: AH=AB+BH
AC=AE+EC
mà AB=AE; BH=EC
nên AH=AC
a. Hình vẽ (0.5 điểm)
Xét ΔABD và ΔAED có:
AB = AE
∠(BAD) = ∠(DAE)
Cạnh AD chung
⇒ ΔABD = ΔAED (c.g.c) (1 điểm)