Tổng tất cả các số tự nhiên n thỏa mãn 1 C n 1 - 1 C n + 2 2 = 7 6 C n + 4 1 là:
A. 11
B. 13
C. 12
D. 10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 2 2017
Để 4n - 1 chai hết cho 7
Thì 4n - 1 thuộc B(7) = {0;7;14;21;28;35;42;................}
Suy ra 4n = {1;8;15;22;29;36;43;50;57;......................}
KK
4
25 tháng 6 2021
`2(n-1)-5(n-2)>0`
`<=>2n-2-5n+10>0`
`<=>8-3n>0`
`<=>3n<8`
`<=>n<8/3`
Mà `n in NN`
`=>n in {0,1,2}`
25 tháng 6 2021
\(2\left(n-1\right)-5\left(n-2\right)>0\)
<=> 2n -2 - 5n + 10 > 0
<=> -3n + 8 > 0
<=> -3n > - 8
<=> \(n< \dfrac{8}{3}\)
Mà n là số tự nhiên
<=> n \(\in\left\{0;1;2\right\}\)
DX
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 10 2023
Vì số tự nhiên cần tìm có đúng 4 ước là
1; a; b; n và n + 1 = 4.( a + b)
Nên n là ước lớn nhất vì vậy n là chính số cần tìm
Vì số ước số của n là 4 và a; b là 2 ước của n nên n = a.b ( a; b \(\in\) P)
Theo bài ra ta có: a.b + 1 = 4.(a + b) ⇒ a.b + 1 = 4.a + 4.b
⇒ a.b - 4a = 4b - 1 ⇒ a.(b - 4) = 4b - 1 ⇒ a = \(\dfrac{4b-1}{b-4}\) ⇒ a = 4 + \(\dfrac{15}{b-4}\)
Vì a \(\in\) P nên b - 4 \(\in\) Ư(15)
Lập bảng ta có:
| b - 4 | -15 | -5 | -3 | -1 | 1 | 3 | 5 | 15 |
| b | -11 (loại) |
-1(loại) |
1 | 3 | 5 | 7 | 9 loại | 19 |
| a = 4 + \(\dfrac{15}{b-4}\) | -1 loại | -11 loại | 19 | 9 loại | 5 |
Theo bảng trên ta có a = 5; b = 19 \(\Rightarrow\) n = 5.19 = 95
Vậy các số tự nhiên thỏa mãn đề bài là 95.
Ghi chú thử lại ta có: 95 = 5.19
Ư(95) = 1; 5; 19; 95 (đúng 4 ước ok)
95 + 1 = 96 = 4.( 5 + 19) (ok)
VV
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 12 2022
6 ⋮ n -2
n- 2 ϵƯ(6) = { -6; -3; -2; -1; 1; 2; 3; 6}
n - 2 = -6 => n = -6 + 2 => n = -4 (loại)
n- 2 = - 3 => n = 2 - 3 => n = -1 (loại)
n- 2 = -2 => n = 2 - 2 => n = 0 (thỏa mãn)
n - 2 = -1 => n = 2 - 1 => n = 1 (thỏa mãn)
n - 2 = 1 => n = 2 + 1 => n = 3 (thỏa mãn)
n - 2 = 2 => n = 2 + 2 => n = 4 (thỏa mãn)
n - 2 = 3 => n = 2 + 3 => n = 5 (thỏa mãn)
n - 2 = 6 => n = 3 + 6 => n = 9 (thỏa mãn)
kết luận n ϵ { 1; 3; 4; 5; 6}
Đáp án A
Phương pháp: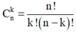
Cách giải: ĐK: n ≥ 1