Tập xác định của hàm số y = x - 2 + 1 x + 2 là:
A. [ - 2 ; + ∞ )
B. ( - 2 ; + ∞ )
C. ( 2 ; + ∞ )
D. [ 2 ; + ∞ )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
PT
1
PT
1
CM
4 tháng 1 2019
Đáp án D
Phương pháp:
Tập xác định của hàm số y = xα:
+) Nếu α là số nguyên dương thì TXĐ: D = R
+) Nếu α là số nguyên âm hoặc bằng 0 thì TXĐ: D = R\{0}
+) Nếu α là số không nguyên thì TXĐ: D = (0;+∞)
Cách giải:
Hàm số xác định ⇔ x + 1 ≠ 0 ⇔ x ≠ -1
Vây tập xác định của hàm số y = (x + 1)-2 là R\{-1}
PT
1
CM
21 tháng 10 2017
+ Với x ≤ 0 thì ta có hàm số 
luôn xác định.
Do đó tập xác định của hàm số 
+Với x> 0 thì ta có hàm số 
luôn xác định.
Do đó tập xác định của hàm số 
Kết hợp cả 2 trường hợp; vậy tập xác định là 
Chọn C.
CM
9 tháng 2 2017
Đáp án A
Áp dụng lý thuyết “lũy thừa với số mũ nguyên âm thì cơ số phải khác 0”
Do đó hàm số y = x − 1 − 2 + log 3 x + 1 xác định khi
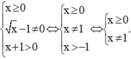
Lỗi sai:
* Các em không nhớ tập xác định của hàm lũy thừa với các trường hợp số mũ khác nhau, ở đây mũ nguyên âm thì cơ số phải khác 0.
* Chú ý (SGK giải tích 12 trang 57). Tập xác định của hàm số lũy thừa y = x α tùy thuộc vào giá trị của α . Cụ thể:
- Với α nguyên dương, tập xác định là R.
- Với α nguyên âm hoặc bằng 0, tập xác định là R\{0}
- Với α không nguyên, tập xác định là 0 ; + ∞
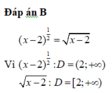
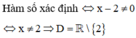
Nhận thấy y = x - 2 + 1 x + 2 có nghĩa khi x - 2 ≥ 0 x + 2 > 0 ⇔ x ≥ 2 x > - 2 ⇔ x ≥ 2 .
Do đó tập xác định của hàm số đã cho là [ 2 ; + ∞ ) .
Vậy đáp án là D.