Phép biến hình biến điểm M thành điểm M’ thì với mỗi điểm M có:
A. Ít nhất một điểm M’ tương ứng
B. Không quá một điểm M’ tương ứng
C. Vô số điểm M’ tương ứng
D. Duy nhất một điểm M’ tương ứng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên không phải là một phép biến hình vì M’không phải là điểm duy nhất được xác định trên mặt phẳng
Ví dụ minh họa: a = 4 cm
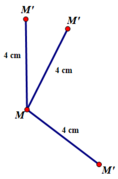

Ta có: \(AM = BM = CN = DN,AN = BN = CM = DM\). Từ đó suy ra
\(\left| {AM - AN} \right| = \left| {BM - BN} \right| = \left| {CM - CN} \right| = \left| {DM - DN} \right| \).
Và \(\left| {AM - AN} \right| <MN\) (bất đẳng thức trong tam giác)
Vậy bốn điểm \(A,B,C,D\) cùng thuộc một đường hyperbol với M,N là hai tiêu điểm.

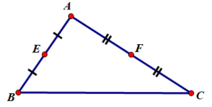
Theo đề bài ta có:
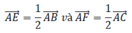
Do đó: Phép vị tự tâm A, tỉ số 1/2 biến điểm B thành điểm E và biến điểm C thành điểm F

Chọn đáp án B
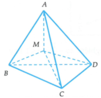
Gọi r1, r2, r3, r4 lần lượt là khoảng cách từ điểm M đến các mặt phẳng (BCD), (ACD), (ABD), (ABC)
Gọi S là diện tích một mặt của tứ diện đều thì
Thể tích tứ diện đều ABCD là V A B C D = a 3 2 12
Ta có V A B C D = V M . B C D + V M . A C D + V M . A B D + V M . A B C
![]()
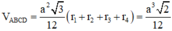
Áp dụng bất đẳng thức Cauchy cho các số dương ta có:
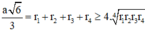
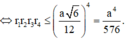
Dấu “=” xảy ra khi và chỉ khi
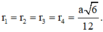

1) Để (d) cắt trục tung tại điểm có tung độ là -1 nên Thay x=0 và y=-1 vào hàm số y=(2m-1)x-3m+5, ta được:
\(\left(2m-1\right)\cdot0-3m+5=-1\)
\(\Leftrightarrow-3m+5=-1\)
\(\Leftrightarrow-3m=-1-5=-6\)
hay m=2(nhận)
Vậy: Khi m=2 thì (d) cắt trục tung tung tại điểm có tung độ bằng -1
quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó gọi là phép biến hình trong mặt phẳng.
chọn đáp án: D