Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc.
DE bằng:
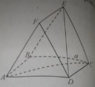
A. a√3
B. a√2
C. 3 a 2
D. a(1 + √3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta tách khối đa diện thành hai phần.
Phần 1. Lăng trụ tam giác DAF.CBE có V = 1 2
Phần 2. Hình chóp tam giác S.CEFD có
V S . C E F D = V B . C E F D = 2 3 V D A F . C B E = 1 3
⇒ V A B C D S E F = 5 6

Ta tách khối đa diện thành hai phần.
Phần 1. Lăng trụ tam giác DAF.CBE có V = 1 2
Phần 2. Hình chóp tam giác S.CEFD có
V S . C D F D = V B . C E F D = 2 3 V D A F . C B E = 1 3 ⇒ V A B C D E F = 5 6
Đáp án cần chọn là D
EB ⊥(ABCD) vì nó vuông góc với giao tuyến AB của hai mặt phẳng vuông góc đã cho ⇒ CD ⊥ (EBC) ⇒ tam giác ECD vuông tại C.
⇒ D E = E C 2 + C D 2 (Áp dụng định lý Py - ta - go)
Ta có: EB ⊥ BC nên tam giác EBC vuông tại B
Suy ra E C = B E 2 + B C 2 = a 2 + a 2 = a 2
Nên ta có: D E = E C 2 + C D 2 = a 2 2 + a 2 = a 3
⇒ DE = a√3.
Vậy phương án A đúng