Hai góc x O y ^ và x ' O y ' ^ đối đỉnh và x O y ^ = 90 o . Chọn câu đúng nh...

PT

Pham Trong Bach

23 tháng 3 2018

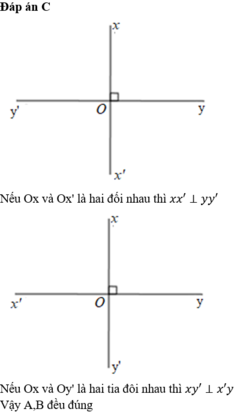
Hai góc x O y ^ và x ' O y ' ^ đối đỉnh và x O y ^ = 90 o . Chọn câu đúng nhất A. x x ' ⊥ y y ' nếu Ox và Ox' là hai tia đối nhau B. x x ' ⊥ y y ' nếu Ox và Oy' là hai tia đối nhau C. Cả A,B đều đúng D. Cả A,B đều...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

23 tháng 3 2018

Đúng(0)

SM

Shimura Mikisa

5 tháng 8 2018 - olm

1,chứng minh hai tia phân giác và đối đỉnh là 2 tia đối nhau

2,cho 2 đg thg xy và zt cắt nhau tại O . Biết xOt = 4 * xOz . Tính các góc tạo thành

3,x* mở ngoặc x-y =3/10 và y* mở ngoặc x-y = -3/50

#Toán lớp 7

0

NC

Nguyễn Cảnh Trung

26 tháng 6 2017 - olm

Cho hai đường thẳng x, x' và y, y' cắt nhau tại O sao cho góc xoy= 40 độ. Các tia Om và On là các tia phân giác của góc xOy, và Ox', Oy'

a, Các tia Om và On có phải là 2 tia đối nhau không

b, Tính số đo của các góc có đỉnh là O

ai trả lời được đúng và nhanh nhất mình sẽ tích

#Toán lớp 7

0

NM

Nhật Minh

3 tháng 11 2023 - olm

Cho hai góc nhọn xOy và x'O'y' có các cạnh tương ứng Ox // O'x' , Oy // O'y'. Vẽ các tia Oz và O'z' lần lượt là phân giác của góc xOy và x'O'y'. Chứng tỏ : a) Hai góc xOy và x'O'y' bằng nhau. b) Oz //...

Đọc tiếp

#Toán lớp 7

2

NT

Nguyễn Thị Thương Hoài

Giáo viên VIP

3 tháng 11 2023

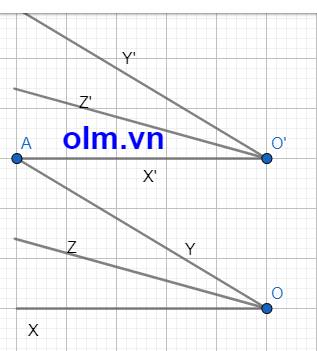
loading...

a,Kéo dài OY cắt O'X' tại A ta có:

\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)

\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)

Kết hợp (1) Và (2) ta có:

\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)

Đúng(0)

NT

Nguyễn Thị Thương Hoài

Giáo viên VIP

3 tháng 11 2023

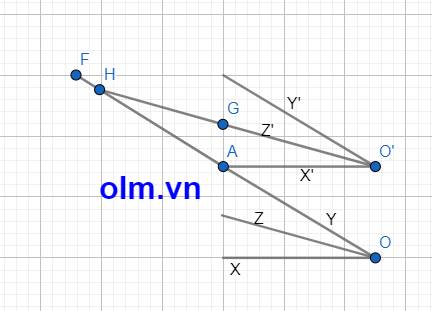
loading...

b, Kéo dài OY cắt O'Z' tại H

\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY

\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')

Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)

\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)

⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)

⇒ OZ // O'Z' (đpcm)

Đúng(0)

PT

Pham Trong Bach

26 tháng 10 2019

Xem hình vẽ và cho biết các khẳng định sau đúng hay sai:A. Hai góc O ^ 1 , O 2 ^ là hai góc đối đỉnh.B. Hai góc O ^ 2 , O 4 ^ là hai góc đối đỉnh.C. Hai góc O ^ 1 , O ^ 4 là hai góc đối đỉnh.D. Hai góc O ^ 3 , O 5 ^ là hai góc đối...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

26 tháng 10 2019

Xem hình vẽ và cho biết các khẳng định sau đúng hay sai:

A. Hai góc O ^ 1 , O 2 ^ là hai góc đối đỉnh. S

B. Hai góc O ^ 2 , O 4 ^ là hai góc đối đỉnh. S

C. Hai góc O ^ 1 , O ^ 4 là hai góc đối đỉnh. Đ

D. Hai góc O ^ 3 , O 5 ^ là hai góc đối đỉnh. S

Đúng(0)

AT

Anh Tran Huynh

21 tháng 9 2021

Mọi người ơi, em cần giải bài này gấp xin mn giúp em

Vẽ hai đường thẳng x,x' và y,y' cắt nhau tại O sao cho góc xOy bằng 60 độ.

a) Viết tên các cặp góc đối đỉnh.

b)Tính số đo các góc còn lại.

#Toán lớp 7

0

AH

An hồ

22 tháng 10 2021

chứng minh rằng "nếu hai góc nhọn xOy và x'O'y'có Ox//O'x'; Oy//O'y' thì xOy = x'O'y' (O' nằm trong góc xOy )

#Toán lớp 7

0

GB

Gia Bảo Trần

2 tháng 10 2021

nếu hai góc nhọn xoy và x'o'y' có ox// với o'x' oy// với o'y' thì xoy = x'o'y'

#Toán lớp 7

0

LA

Lan Anh

24 tháng 4 2018 - olm

1)Cho góc xOy có số đo bằng 90 độ .vẽ tia oz nằm giữa hai tia Ox và Oy sao cho góc x o t = 30 độ

A) tính số đo góc yOt

B) hỏi đi ô tô có phải là tia phân giác của góc x O y k ?vì sao?

2) Cho hai góc kề bù x O y và yox', biết góc xOy = góc yOx'. Chứng tỏ góc xOy là góc vuông.

#Toán lớp 6

1

HH

hoàng hà phương ánh

24 tháng 4 2018

a)góc yot =60 độ b)ko,vì xot và yot ko = nhau

Đúng(0)

ML

Minh Lệ

22 tháng 8 2023

Chọn câu trả lời đúng.

Bạn Rô-bốt vẽ góc đỉnh O; cạnh OM, ON có số đo 30° và góc đỉnh O; cạnh ON, OP có số đo 90° để tạo thành góc đỉnh O; cạnh OM, OP. Hỏi hình nào sau đây là hình Rô-bốt đã vẽ?

#Toán lớp 4

1

NV

Nguyễn Việt Dũng

CTVVIP

22 tháng 8 2023

Đáp án đúng là: B

+ Ở hình A, góc đỉnh O; cạnh OM, ON bằng 90⁰nên không phải là hình Rô-bốt vẽ.

+ Ở hình C, góc đỉnh O; cạnh ON, OP là góc nhọn nên cũng không phải là hình Rô-bốt vẽ.

Vậy hình B là hình Rô-bốt đã vẽ.

Đúng(2)

TM

Trương Mỹ Hoa

25 tháng 10 2023

1) Vẽ hai đường thẳng x x' & y y' cắt nhau tại O.
a) Viết tên các cặp góc đối đỉnh
b) Viết tên các cặp góc bù nhau
2) Vẽ góc xoy=30^o. Vẽ góc yoy kề bù với góc xoy ; vẽ góc yox đối đỉnh góc xoy
a) Tính số đo góc yoy
b) Tính số đo góc xox

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

25 tháng 10 2023

1:

a: Hai cặp góc đối đỉnh là \(\widehat{xOy};\widehat{x'Oy'}\) và \(\widehat{xOy'};\widehat{x'Oy}\)

b: hai cặp góc bù nhau là:

\(\widehat{xOy};\widehat{xOy'}\)

\(\widehat{x'Oy};\widehat{x'Oy'}\)

loading...

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP