Cho hình lăng trụ đứng ABCD.MNPQ có đáy hình thang AB// CD và AB = 4cm; CD = 6cm và chiều cao của hình thang là 5cm, chiều cao của hình lăng trụ là: 4cm. Tính thể tích của hình lăng trụ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu vi đáy là:
P = 2(AB + BC) = 2.(6 + 4) = 20cm
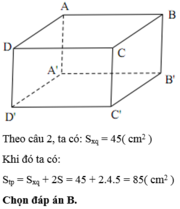
Diện tích xung quanh của hình lăng trụ đã cho là:
S x q = P . h = 20 . 5 = 100 ( c m 2 )
Chọn đáp án A

a) Tính được A P = 74 c m v à A O = 221 2 c m
b) Ta tính được AD = 4cm, từ đó tính được tổng diện tích hai mặt đáy là 24cm2

\(BC=\sqrt{4^2-3^2}=\sqrt{7}\left(cm\right)\)
\(S_{Xq}=\left(3+\sqrt{7}\right)\cdot5=15+5\sqrt{7}\left(cm^2\right)\)
\(V=3\cdot\sqrt{7}\cdot5=15\sqrt{7}\left(cm^3\right)\)

Đáp án A
Từ giả thiết ta có hình thang ABCD là hình thang nội tiếp được đường tròn nên nó là hình thang cân AB = AD = BC = a
Khi đó tâm đường tròn ngoại tiếp hình thang ABCD là trung điểm I của CD và bán kính là r = a.
Ta có:
![]()
=> A'A = a 3 . 3 = 3a => V = 3π a 3
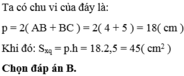
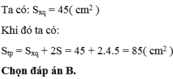

Chọn đáp án C