Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
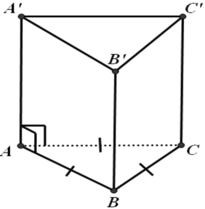
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2

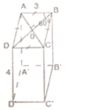
a) Sxq = 2.P.H (p: chu vi đáy; h: chiều cao)
= 3(3 + 3).4 = 48(cm2)
b) Gọi O là giao điểm của AC và BD. Vì tứ giác ABCD là hình thoi nên AC ⊥ BD tại O và có ∠ABC = 60o => ∠ABO = 30o
ΔABO là nửa tam giác đều nên
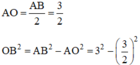
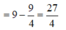
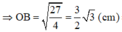
![]()
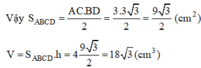

Xét tam giác ABC có nửa chu vi của tam giác là:
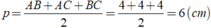
Khi đó ta có
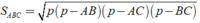

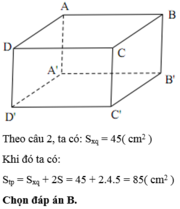
+ Diện tích xung quanh của hình lăng trụ


Chu vi đáy là:
P = 2(AB + BC) = 2.(6 + 4) = 20cm
Diện tích xung quanh của hình lăng trụ đã cho là:
S x q = P . h = 20 . 5 = 100 ( c m 2 )
Chọn đáp án A

BC=căn 6^2+8^2=10cm
Sxq=(6+8+10)*10=240cm2
Stp=240+2*6*8/2=288cm2
V=1/2*6*8*10=240cm3
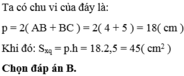

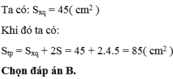
\(BC=\sqrt{4^2-3^2}=\sqrt{7}\left(cm\right)\)
\(S_{Xq}=\left(3+\sqrt{7}\right)\cdot5=15+5\sqrt{7}\left(cm^2\right)\)
\(V=3\cdot\sqrt{7}\cdot5=15\sqrt{7}\left(cm^3\right)\)