Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Mặt phẳng đi qua A’B’ và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Tính thể tích hình chóp C.A’B’FE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 11 2018
Đáp án A
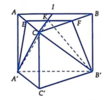
Gọi K là trọng tâm tam giác ABC. Qua K kẻ đường thẳng song song với A'B' lần lượt cắt AC; BC tại E và F. Gọi I là giao của CK và AB. Ta có
C I ⊥ A B B ' A ' ⇒ V C B A ' B ' = 1 3 . C I . S B A ' B ' = 1 3 . a 3 2 . a 2 2 = a 3 13 12 .
Kí hiệu như hình vẽ. Ta có V = V C F A ' B ' + V C E A ' F .
Mà V C E A ' F C A ' B B ' = 2 3 . 2 3 . 1 ⇒ V C E A ' F = 4 9 . 1 3 . A A ' . S A B C = 4 27 . a . a 2 3 4 = a 3 3 27 .
V C F A ' B ' C B A ' B ' = 2 3 . 1 . 1 ⇒ V C F A ' B ' = 2 3 . a 3 3 12 = a 3 13 18 . Suy ra V = a 3 3 27 + a 3 3 18 = 5 a 3 3 54 .
1 tháng 4 2017
Ta tính thể tích hình chóp A’.BCB’. Gọi M là trung điểm của B’C’, ta có: ATM ⊥ B’C’ (1)
Lăng trụ ABC.A’B’C’ là lăng trụ đứng nên: BB’ ⊥ (A’B’C’) ⇒BB’⊥ A’M (2)
Từ (1) và (2) suy ra
AM⊥ (BB’C) hay A’M là đường cao của hình chóp A’.BCB’
CM
25 tháng 1 2017
Đáp án B
Phương pháp giải:
Dựng hình, xác định khoảng cách giữa hai đường thẳng chéo nhau để tính chiều cao lăng trụ
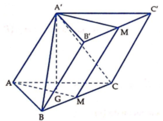
Lời giải: Gọi M là trung điểm của BC.
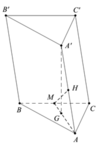
Ta có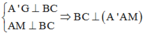 
Kẻ 
=> MH là đoạn vuông góc chung của BC, AA’
Mà 
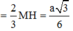
Xét tam giác vuông AA’G có :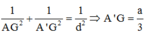 
Vậy thể tích cần tính là: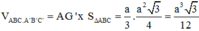 
CM
24 tháng 7 2019
Chọn D
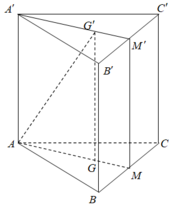
Gọi M, M' lần lượt là trung điểm của BC và B’C’. Khi đó thiết diện của lăng trụ tạo bởi mặt phẳng (AGG') là hình chữ nhật AMM'A’.
Mà A M ’ = a . s i n 60 0 = a 3 2 ≠ A A ’
Nên AMM’A’ không thể là hình vuông.
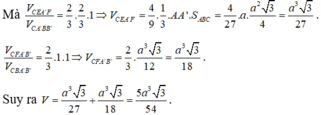
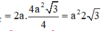
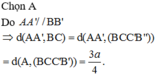
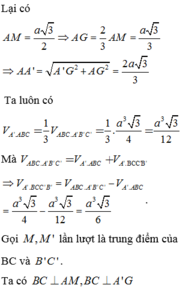
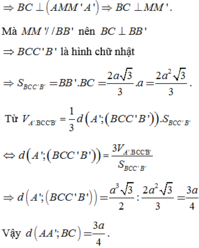
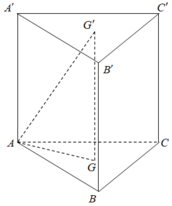
Gọi I, K lần lượt là trung điểm của AB và A’B’, G là trọng tâm của tam giác ABC.Đường thẳng qua G, song song với AB cắt AC và BC lần lượt tại E và F, đường thẳng EF chính là giao tuyến của hai mặt phẳng (GA’B’) và (ABC).