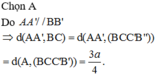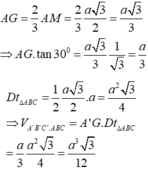Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp giải:
Dựng hình, xác định khoảng cách giữa hai đường thẳng chéo nhau để tính chiều cao lăng trụ
Lời giải: Gọi M là trung điểm của BC.
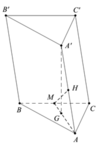
Ta có 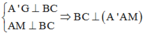
Kẻ ![]() => MH là đoạn vuông góc chung của BC, AA’
=> MH là đoạn vuông góc chung của BC, AA’
![]()
Mà ![]()
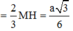
Xét tam giác vuông AA’G có : 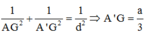
Vậy thể tích cần tính là: 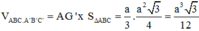

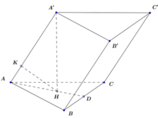
Gọi D là trung điểm của BC, H là chân đường cao kẻ từ A’ đến , và K là chân đường cao kẻ từ H đến AA’. Dễ thấy khoảng cách từ BC đến AA’ bằng với khoảng cách từ D đến AA’ và bằng 3/2d(H,AA’).
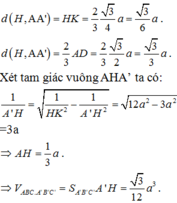
Đáp án D

Đáp án C
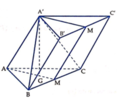
Ta dễ dàng chứng minh được A A ' / / B C C ' B '
⇒ d A A ' ; B C = d A A ' ; B C C ' B ' = d A ; B C C ' B '
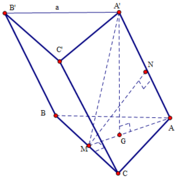
Gọi G là trọng tâm của tam giác ABC. Suy ra A ' G ⊥ A B C .
Ta có S Δ A B C = a 2 3 4
⇒ V A B C . A ' B ' C ' = A ' G . S Δ A B C ⇔ A ' G = V A B C . A ' B ' C ' S Δ A B C = a 3 3 4 : a 2 3 4 = a
Lại có
A M = a 3 2 ⇒ A G = 2 3 A M = a 3 3 ⇒ A A ' = A ' G 2 + A G 2 = 2 a 3 3
Ta luôn có V A ' . A B C = 1 3 V A B C . A ' B ' C ' = 1 3 . a 3 3 4 = a 3 3 12 .
Mà V A B C . A ' B ' C ' = V A ' . A B C + V A ' . B C C ' B '
⇒ V A ' . B C C ' B ' = V A B C . A ' B ' C ' − V A ' . A B C = a 3 3 4 − a 3 3 12 = a 3 3 6 .
Gọi M,M' lần lượt là trung điểm của BC và B'C'. Ta có B C ⊥ A M , B C ⊥ A ' G ⇒ B C ⊥ A M M ' A ' ⇒ B C ⊥ M M ' . Mà M M ' / / B B ' nên B C ⊥ B B ' ⇒ B C C ' B ' là hình chữ nhật
⇒ S B C C ' B ' = B B ' . B C = 2 a 3 3 . a = 2 a 2 3 3 .
Từ
V A ' . B C C ' B ' = 1 3 d A ' ; B C C ' B ' . S B C C ' B ' ⇔ d A ' ; B C C ' B ' = 3 V A ' . B C C ' B ' S B C C ' B '
⇒ d A ' ;...

Đáp án D
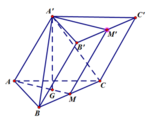
Ta có d ( AA ' , B C ) = d ( A A ' , ( B B ' C ' C ) ) = d ( A ' , ( B B ' C ' C ) )
Gọi M và M’ lần lượt là trung điểm BC và B’C’, G là trọng tâm của tam giác ABC
Theo giả thiết ta có B C ⊥ A M B C ⊥ A ' G ⇒ B C ⊥ ( A A ' G ) ⇒ B C ⊥ A A ' , nên tứ giác BB’C’C là hình chữ nhật có cạnh BC = a
Vì
V A ' A B C = 1 3 A ' G . S Δ A B C = 1 3 V L T = a 3 3 12 ⇒ A ' G = a ⇒ A A ' = A G 2 + A ' G 2 = 2 a 3
Có
V A ' B B ' C ' C = 2 3 V L T = a 3 3 6 = 1 3 d ( A ' , ( B B ' C ' C ) ) . S B B ' C ' C ⇒ d ( A ' , ( B B ' C ' C ) ) = 3 a 2

Đáp án D
Ta có d ( AA ' , B C ) = d ( A A ' , ( B B ' C ' C ) ) = d ( A ' , ( B B ' C ' C ) )
Gọi M và M’ lần lượt là trung điểm BC và B’C’, G là trọng tâm của tam giác ABC
Theo giả thiết ta có B C ⊥ A M B C ⊥ A ' G ⇒ B C ⊥ ( A A ' G ) ⇒ B C ⊥ A A ' , nên tứ giác BB’C’C là hình chữ nhật có cạnh BC = a
Vì
V A ' A B C = 1 3 A ' G . S Δ A B C = 1 3 V L T = a 3 3 12 ⇒ A ' G = a ⇒ A A ' = A G 2 + A ' G 2 = 2 a 3
⇒ S B B ' C ' C = 2 a 2 3
Có V A ' B B ' C ' C = 2 3 V L T = a 3 3 6 = 1 3 d ( A ' , ( B B ' C ' C ) ) . S B B ' C ' C ⇒ d ( A ' , ( B B ' C ' C ) ) = 3 a 2
Chọn D

Đáp án A
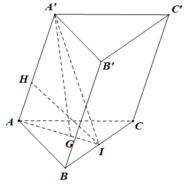
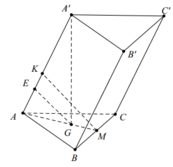
Gọi I là trung điểm của BC.
Vì B C ⊥ A ' G B C ⊥ A I ⇒ B C ⊥ A A ' I
Hạ I H ⊥ A A ' ⇒ I H ⊥ B C
⇒ d A A ' ; B C = I H = a 3 4 A I = a 3 2 ⇒ A H = A I 2 − H I 2 = 3 a 4 A G = 2 3 A I = a 3 3 A ' G = A G . tan A ' A G = a 3 3 . H I A H = a 3 3 a 3 4 3 a 4 = a 3 V A B C . A ' B ' C ' = A ' G . S A B C = a 3 . a 2 3 4 = a 3 3 12