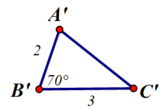
Vẽ thêm tam giác A’B’C’ có :
A’B’ = 2cm ; ∠B' = 70o; B’C’ = 3cm
Hãy đo để kiểm nghiệm rằng AC = A’C’. Ta có thể kết luận được tam giác ABC bằng tam giác A’B’C’ hay không ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 5 2019
Hai tam giác trên có :
∠A = ∠A' ; ∠B = ∠B' ; ∠C = ∠C'
Nhận xét: Hai tam giác trên bằng nhau
CM
19 tháng 11 2017
ΔABC và ΔA’B’C’ có:
AB = A’B’
∠B = ∠B'
BC = B’C’
⇒ ΔABC = ΔA’B’C’ (cạnh – góc – cạnh)
CM
13 tháng 9 2019
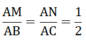
⇒ MN // BC (định lí Ta lét đảo)
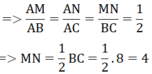
Suy ra: Δ AMN = ∆ A’B’C’(c.c.c) nên hai tam giác này cũng đồng dạng với nhau (1).
Xét tam giác ABC có MN// BC nên Δ AMN đồng dạng với tam giác ABC (2)
Từ (1) và (2) suy ra: Δ A’B’C’ đồng dạng với tam giác ABC (tính chất).
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
- Độ dài các cạnh tương ứng của 2 tam giác ABC và A’B’C’ bằng nhau.
- Hai tam giác ABC và A'B'C' có bằng nhau.
- Độ dài các cạnh AB' và AC' của hai tam giác em vừa vẽ có bằng các cạnh AB' và AC' của hai tam giác các bạn khác vẽ.
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ.
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Tam giác ABC có bằng tam giác A’B’C’ (vì 2 tam giác này có thể chồng khít lên nhau).
17 tháng 9 2023
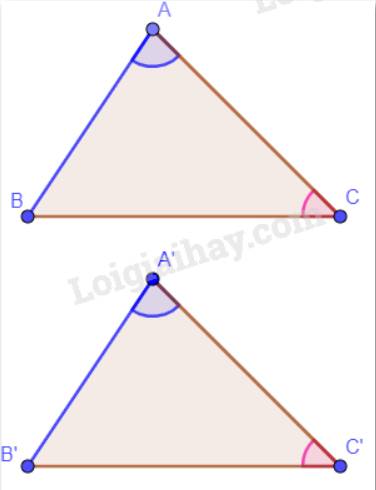
Vì \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\)mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat {B'}\).
Xét hai tam giác ABC và A’B’C’ có: \(\widehat A = \widehat {A'}\), AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
CM
11 tháng 4 2017
* Trong tam giác vuông A’B’C’ có ∠ A ' = 90 0
Áp dụng định lí Pi-ta-go, ta có: A ' B ' 2 + A ' C ' 2 = B ' C ' 2
Suy ra: A ' C ' 2 = B ' C ' 2 - A ' B ' 2 = 15 2 - 9 2 = 144
Suy ra: A’C’ = 12 (cm)
* Trong tam giác vuông ABC có ∠ A = 90 0
Áp dụng định lí Pi-ta-go, ta có: B C 2 = A B 2 + A C 2 = 6 2 + 8 2 =100
Suy ra: BC = 10 (cm)
Ta có: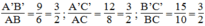 
Suy ra: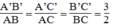 
Vậy △ A’B’C’ đồng dạng ΔABC (c.c.c)
Ta có thể kết luận được tam giác ABC bằng tam giác A’B’C’ (trường hợp c.g.c)