Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Trong tam giác vuông A’B’C’ có \(\widehat{A'}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
A′B′2+A′C′2 =B′C′2
=> A′C′2=B′C′2−A′B′2=152−92=144
=> A’C’ =12 (cm)
Trong tam giác vuông ABC có \(\widehat{A}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
BC2=AB2+AC2= 62+82=100
Suy ra: BC = 10 (cm)
Ta có: \(\dfrac{A'B'}{AB}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(\dfrac{A'C'}{AC}=\dfrac{12}{8}=\dfrac{3}{2}\)
\(\dfrac{B'C'}{BC}=\dfrac{15}{10}=\dfrac{3}{2}\)
Suy ra: \(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{B'C'}{BC}=\dfrac{3}{2}\)
Vậy ∆ A’B’C’ đồng dạng với ∆ ABC

Xét \(\Delta ABC\)vuông tại A theo định lí Pitago ta có : \(AB^2+AC^2=BC^2\Rightarrow6^2+8^2=BC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét \(\Delta DEF\)vuông tại D theo định lí Pitago ta có :\(DE^2+DF^2=EF^2\)
=> \(DF^2=EF^2-DE^2=15^2-9^2=144\)
=> \(DF=\sqrt{144}=12\left(cm\right)\)
Để hai tam giác trên đồng dạng với nhau , trước hết tính tỉ lệ tương ứng với 3 cạnh
Xét tam giác ABC và tam giác DEF ta có :
\(\frac{AB}{DE}=\frac{6}{9}=\frac{2}{3}\)
\(\frac{BC}{EF}=\frac{10}{15}=\frac{2}{3}\)
\(\frac{AC}{DF}=\frac{8}{12}=\frac{2}{3}\)
=> \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\left(=\frac{2}{3}\right)\)
=> Tam giác ABC đồng dạng tam giác DEF
Nếu bạn muốn làm tam giác DEF đồng dạng với tam giác ABC cũng được

a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)

* Trong tam giác vuông A’B’C’ có ∠ A ' = 90 0
Áp dụng định lí Pi-ta-go, ta có: A ' B ' 2 + A ' C ' 2 = B ' C ' 2
Suy ra: A ' C ' 2 = B ' C ' 2 - A ' B ' 2 = 15 2 - 9 2 = 144
Suy ra: A’C’ = 12 (cm)
* Trong tam giác vuông ABC có ∠ A = 90 0
Áp dụng định lí Pi-ta-go, ta có: B C 2 = A B 2 + A C 2 = 6 2 + 8 2 =100
Suy ra: BC = 10 (cm)
Ta có: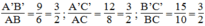
Suy ra: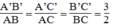
Vậy △ A’B’C’ đồng dạng ΔABC (c.c.c)