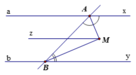
Cho hình vẽ bên, biết a x / / b y .Hai tia phân giác của x A B ^ và A B y ^ cắt nhau tại M. Chứng minh A M ⊥ B M
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
12 tháng 3 2018
a) Theo đề bài ta có: \(\widehat{DAF}+\widehat{ADF}=\frac{\widehat{DAB}+ADC}{2}=\frac{180^o}{2}=90^o\)
Xét tam giác AFD có \(\widehat{DAF}+\widehat{ADF}=90^o\) nên \(\widehat{AFD}=90^o\)
Hay tam giác AFD vuông tại F.
Gọi E là trung điểm AD.
Xét tam giác vuông ADF có FE là trung tuyến ứng với cạnh huyền nên EF = AD/2
Lại có do F là trung điểm BC; E là trung điểm AD nên EF là đường trung bình hình thang.
Từ đó suy ra \(EF=\frac{AB+BC}{2}\)
Vậy nên AD = AB + BC.
b) Giả sử AD = AE + ED.
Gọi E là trung điểm AD. Do AD = AB + CD nên FE = (AB + DC)/2
Ta có E là trung điểm AD. Vậy nên EF là đường trung bình hình thang hay hay Flà trung điểm BC.
15 tháng 9 2019
Tham khảo : Câu hỏi của Trần Nhật Duy - Toán lớp 8 - Học toán với OnlineMath
Kẻ M z / / a x / / b y
Vì AM là tia phân giác của x A B ^
⇒ A M z ^ = x A M ^ = 1 2 x A B ^
BM là phân giác của A B y ^
⇒ A B M ^ = M B y ^ = 1 2 A B y ^
Ta có: M z / / a x nên A M z ^ = M A x ^ (hai góc so le trong)
M z / / b y nên z M B ^ = B M y ^ (hai góc so le trong)
⇒ A M B ^ = A M z ^ + z M B ^ = 1 2 x A B ^ + A B y ^ = 1 2 ⋅ 180 0 = 90 0
Vậy A M ⊥ B M (đpcm)