Chứng minh D Ax ^ = B C N ^ theo nhiều cách
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 4 2019
Đúng(0)
Những câu hỏi liên quan
CM
22 tháng 10 2019
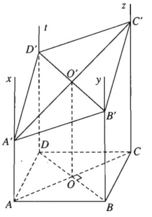
a) Ta có hai mặt phẳng song song là: (Ax, AD) // (By, BC)
Hai mặt phẳng này bị cắt bởi mặt phẳng (β) nên ta suy ra các giao tuyến của chúng phải song song nghĩa là A′D′ // B′C′.
Tương tự ta chứng minh được A′B′ // D′C′. Vậy A', B', C', D' là hình bình hành. Các hình thang AA'C'C và BB'D'D đều có OO' là đường trung bình trong đó O là tâm của hình vuông ABCD và O' là tâm của hình bình hành A',B',C',D'. Do đó: AA′ + CC′ = BB′ + DD′ = 2OO′
b) Muốn hình bình hành A',B',C',D' là hình thoi ta cần phải có A'C' ⊥ B'D'. Ta đã có AC ⊥ BD. Người ta chứng minh được rằng hình chiếu vuông góc của một góc vuông là một góc vuông khi và chỉ khi góc vuông đem chiếu có ít nhất một cạnh song song với mặt phẳng chiếu hay nằm trong mặt chiếu. Vậy A', B', C', D' là hình thoi khi và chỉ khi A'C' hoặc B'D' song song với mặt phẳng (α) cho trước. Khi đó ta có AA' = CC' hoặc BB' = DD'.
c) Muốn hình bình hành A', B', C', D' là hình chữ nhật ta cần có A'B' ⊥ B'C', nghĩa là A'B' hoặc B'C' phải song song với mặt phẳng (α)(α). Khi đó ta có AA' = BB' hoặc BB' = CC', nghĩa là hình bình hành A', B', C', D' có hai đỉnh kề nhau cách đều mặt phẳng (α) cho trước.
DD
Đoàn Đức Hà
Giáo viên
26 tháng 12 2022
Gợi ý:
a) Có \(A,M\) cùng nhìn \(CO\) dưới góc \(90^o\) nên \(A,C,M,O\) cùng thuộc một đường tròn.
b) \(CA=CM,DB=DM\) (tính chất hai tiếp tuyến cắt nhau)
Xét tam giác \(COD\) vuông tại \(O\) đường cao \(OM\):
\(OM^2=CM.DM=AC.BD\).
c) Kẻ \(MH\perp AB\). Kéo dài \(BM\) cắt \(Ax\) tại \(E\).
Tam giác \(AME\) vuông tại \(M\) có \(CM=CA\) do đó \(C\) là trung điểm của \(AE\).
Suy ra \(BC\) đi qua trung điểm của \(MH\).
Tương tự ta cũng chứng minh được \(AD\) đi qua trung điểm của \(MH\).
Vậy \(M,N,H\) thẳng hàng suy ra \(MN\perp AB\).
d) Ta có \(\dfrac{OC^2.OD^2}{CD^3}=\dfrac{\left(OC.OD\right)^2}{CD^3}=\dfrac{\left(OM.CD\right)^2}{CD^3}=\dfrac{OM^2}{CD}\).
\(\dfrac{DM}{DC}=\dfrac{MN}{AC},\dfrac{CM}{DC}=\dfrac{MN}{BD}\) suy ra \(\dfrac{DM+CM}{DC}=MN\left(\dfrac{1}{AC}+\dfrac{1}{BD}\right)\)
\(\Leftrightarrow MN=\dfrac{AC.BD}{AC+BD}=\dfrac{OM^2}{CD}\).
Suy ra đpcm.
DT
20 tháng 12 2017
Đây nhé
a, Ta có Xét tam giác ABC có:
OC là trung tuyến của tam giác ABC
OC=OA=OB
Suy ra tam giác ABC vuông tại C
Vậy AC vuông góc với MB
b,Xét tam giác AMB vuông tại A có AC là đường cao
suy ta BC.BM=AB^2=4R^2(hệ thức lượng tam giác vuông )
c,Ta có:
TAm giác ADO cân tại O có OH là đường cao
suy ra H:trung điểm AD
suy ra tam giác AMD cân tại M
suy ra AM=MD
Tam giác AMB vuông tại A có đường cao AC
suy ra AM^2=MC.MB(hệ thức luợng tam giác vuông)
Suy ra MD^2=MC.MB
Nhận xét: Câu c là phương tích trong đường tròn
31 tháng 8 2022
a: Xét (O) có
CA,CE là các tiếp tuyến
nên CA=CE và OC là phân giác của góc AOE(1)
Xét (O) có
DE,DB là các tiếp tuyến
nên DE=DB và OD là phân giác của góc EOB(2)
Ta có: CE+ED=CD
nên CD=CA+DB
b: Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\left(\widehat{EOA}+\widehat{EOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
c: \(AC\cdot BD=CE\cdot ED=OE^2=R^2\)
d: Gọi M là trung điểm của CD
Xét tứ giác ACDB có
O,M lần lượt là trung điểm của AB và CD
nên OM là đường trung bình
=>OM//AC//BD
hay OM vuông góc với AB
Vì ΔCOD vuông tại O
mà M là trung điểm của CD
nên M là tâm đường tròn ngoại tiếp ΔCOD
=>AB là tiếp tuyến tại O của (M)