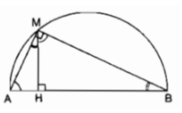
Cho một nửa đường tròn đường kính AB. Điểm M chạy trên nửa đường tròn. Kẻ MH vuông góc với AB tại H. Đặt MH = x. Chứng minh rằng AH.BH = M H 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

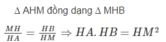

Với mỗi giá trị của x ta có một giá trị xác định của P(x).
Vậy P(x) là một hàm số.
P(x) = x 2

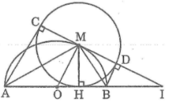
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = AH và BD = BH
Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH
Suy ra: AC + BD = AH + BH = AB không đổi

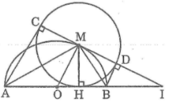
Ta có: AC ⊥ CD và BD ⊥ CD (tính chất tiếp tuyến)
Suy ra: AC // BD hay tứ giác ABDC là hình thang
Mà OA = OB (bán kính (O))
Và AC = MD (bán kính (M))
Suy ra OM là đường trung bình của hình thang ABDC
Khi đó OM // AC. Suy ra: OM ⊥ CD hay góc (OMI) = 90 °
Tam giác OMI vuông tại M có MH ⊥ OI
Theo hệ thức lượng trong tam giác vuông ta có: O M 2 = OH.OI
Suy ra: OH.OI = R 2 không đổi.