Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B M C D E H
Câu c: \(BM\) cắt \(AC\) tại \(E\). Như vậy thì tam giác \(EMA\) vuông tại \(M\).
\(CA=CM\) nên \(\widehat{EAM}=\widehat{CMA}\).
Mà \(\widehat{EAM}+\widehat{AEB}=90^o=\widehat{CMA}+\widehat{EMC}\) nên \(\widehat{AEM}=\widehat{EMC}\).
Tức là \(CE=CM=CA\) hay \(C\) là trung điểm \(AM\)
Đến đây bạn để ý \(MH\) song song với \(AM\) và dùng định lí Thales là CM được.
Gọi N là giao MH với BC ( N thuộc MH )
Tương tựTrần Quốc Đạt thì C là trung điểm AE
Vì MN // CE nên theo Ta-let
\(\frac{MN}{CE}=\frac{BN}{BC}\)
Vì NH // CA nên theo Talet
\(\frac{BN}{BC}=\frac{NH}{CA}\)
\(\Rightarrow\frac{MN}{CE}=\frac{NH}{CA}\)
Mà CE = CA (trung điểm)
\(\Rightarrow MN=NH\)=> N là trung điểm MH
Nên BC đi qua trung điểm N của MH
P/S : BÀi này ko liên quan tới A,N,D thẳng hàng nhé !

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC

Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = AC, DM = BC
Do đó: CD = CM + DM = AC + BD (đpcm)

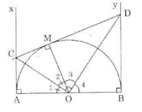
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OC là tia phân giác của ∠AOM
OD và tia phân giác của ∠BOM
OC và OD là các tia phân giác của hai góc kề bù ∠AOM và ∠BOM nên OC ⊥ OD.
=> ∠COD = 90o (đpcm)