Có 5 nữ và 6 nam xếp thành một hàng dọc sao cho đầu hàng và cuối hàng luôn là nữ. Hỏi có bao nhiêu cách xếp?
A. 362880
B. 806400
C. 7257600
D. 151280
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 9 2019
Số cách chọn 2 nam đứng ở đầu và cuối là 
.
Lúc này còn lại 5 nam và 5 nữ, để đưa 10 người này vào hàng thì trước tiên sẽ cho 5 nam đứng riêng thành hàng ngang, số cách đứng là 5!. Sau đó lần lượt “nhét” 5 nữ vào các khoảng trống ở giữa hoặc đầu, hoặc cuối của hàng 5 nam này, mỗi khoảng trống chỉ “nhét” 1 nữ hoặc không “nhét”, có tất cả 6 khoảng trống nên số cách xếp vào là 
.
Số cách xếp 10 người này thành hàng ngang mà 2 nữ bất kì không đứng cạnh nhau là:
Đưa 10 người này vào giữa 2 nam đầu và cuối đã chọn, số cách xếp là:
Chọn D.
CM
2 tháng 9 2019
- Nếu đánh số theo hàng dọc từ 1 đến 9 thì cần xếp 5 học nữ vào 5 vị trí lẻ nên có 5!cách xếp; và xếp 4 học sinh nam vào 4 vị trí chẵn nên có 4!cách xếp. Theo quy tắc nhân ta có, ta có 4!*5! Cách xếp 9 học sinh thành hàng dọc xen kẽ nam nữ.
Chọn A
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2023
Xếp thứ tự 7 nam: có \(7!\) cách
7 nam tạo thành 8 khe trống, loại ra 2 khe trống bên ngoài 2 nam ngoài cùng, xếp 3 nữ vào 6 khe trống còn lại: \(A_6^3\) cách
Vậy tổng cộng có: \(7!.A_6^3\) cách xếp thỏa mãn
C
11 tháng 3 2023
Anh giúp em ạ! Anh làm theo cách gì hay và nhanh nhá anh, vì anh có nhiều cách hay lắm, em toàn nghĩ theo cách nguyên thủy
https://hoc24.vn/cau-hoi/cho-tap-hop-x-gom-0-1-2-3-4-5-6-7-8-9-lap-duoc-bao-nhieu-so-tu-nhien-co-4-chu-so-sao-cho-co-2-chan-va-2-le.7748017658781
21 tháng 1 2022
Số cách xếp 4 bạn nữ đứng cạnh nhau : \(4!\) (cách)
Số cách xếp 6 bạn nam đứng cạnh nhau : \(6!\left(cách\right)\)
Đổi chỗ nam và nữ có : \(2\) (cách)
\(\Leftrightarrow\) Số cách xếp : \(2.4!.6!\) (cách)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2022
Xếp 4 nữ cạnh nhau: 4! cách
Coi 4 nữ như 1 bạn, hoán vị cùng 6 bạn nam: 7! cách
Tổng cộng: \(4!.7!\) cách
TH
Thầy Hùng Olm
Manager
VIP
12 tháng 5 2023
Vị trí các bạn nữ theo dãy số cách đều:
1; 6; 11; ... 56
Số bạn nữ là số lượng số của dãy cách đều 5 đơn vị
Số các bạn nữ là: (56 - 1): 5 + 1 = 12 (bạn)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 5 2023
Thêm hay bớt bao nhiêu bạn nữ thì số bạn nam cũng luôn luôn không đổi.
Nếu ta trừ ra bạn nữ cuối cùng thì tổng số học sinh trong hàng lúc sau là:
56 - 1 = 55 (bạn)
Cứ 1 bạn nữ thì có 4 bạn nam đứng sau nên tỉ số bạn nữ lúc sau so với bạn nam là:
1 : 4 = \(\dfrac{1}{4}\)
Ta có sơ đồ:
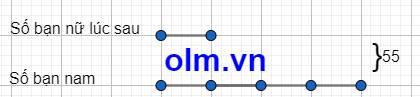
Theo sơ đồ ta có:
Số bạn nữ lúc sau là: 55 : ( 4 + 1) = 11 (bạn)
Số bạn nữ lúc đầu là: 11 + 1 = 12 ( bạn)
Đáp số: 12 bạn
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1
a.
Xếp 4 bạn nữ cạnh nhau: \(4!\) cách
Coi 4 bạn nữ là 1 bạn, xếp với 6 bạn nam: \(7!\) cách
Theo quy tắc nhân ta có: \(4!.7!\) cách
b.
Xếp 6 bạn nam: \(6!\) cách
6 bạn nam tạo thành 7 khe trống, xếp 4 nữ vào 7 khe trống này: \(C_7^4\) cách
\(\Rightarrow6!.C_7^4\) cách
c. Do có 6 nam và 4 nữ nên ko thể tồn tại cách xếp xen kẽ nam nữ (luôn có ít nhất 2 nam đứng cạnh nhau)
d.
Xếp 4 nữ cạnh nhau: \(4!\) cách
Xếp 6 nam cạnh nhau: \(6!\) cách
Hoán vị nhóm nam và nữ: \(2!\) cách
\(\Rightarrow4!.6!.2!\) cách
Số cách chọn 2 bạn nữ xếp ở vị trí đầu hàng và cuối hàng là: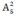
(ở đây ta xem cách xếp 1 bạn nữ A ở đầu hàng, bạn nữ B ở cuối hàng với cách xếp bạn nữ A ở cuối hàng, bạn nữ B ở đầu hàng là khác nhau).
Lúc này, còn lại 3 bạn nữ và 6 bạn nam, số cách xếp 9 người này vào 1 hàng là: 9!.
Vậy số cách xếp thỏa yêu cầu đề là: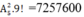
Chọn C