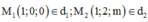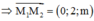Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng 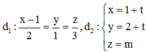.Gọi S là tập hợp tất cả các số m sao cho đường thẳng d1và d2 chéo nhau và khoảng cách giữa chúng bằng
5
19
. Tính tổng các phần tử của S A. 11 B. 12 C. 12 D.
-
...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng 
.Gọi S là tập hợp tất cả các số m sao cho đường thẳng d1và d2 chéo nhau và khoảng cách giữa chúng bằng
5
19
. Tính tổng các phần tử của S
A. 11
B. 12
C. 12
D. - 11
là 1 VTCP
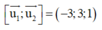
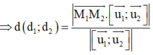
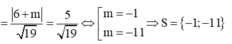
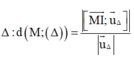
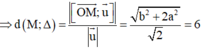
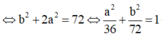
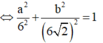
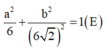
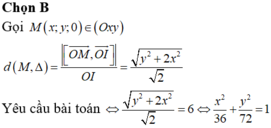
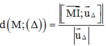
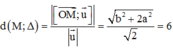
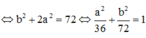
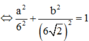
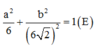
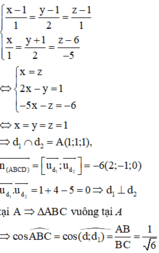
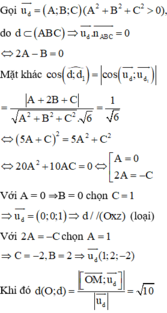
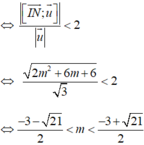
Đáp án B
Phương pháp: Sử dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau:
Với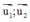
lần lượt là các VTCP của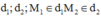 
Cách giải:
Ta có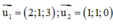
lần lượt là các VTCP của d1; d2
Ta có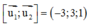
Lấy
