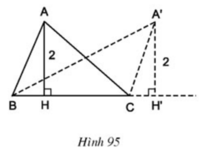
Xét các tam giác ABC có BC cố định, đường cao ứng với cạnh BC luôn bằng 2 cm (h.95). Đỉnh A của các tam giác đó nằm trên đường nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em có thể tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuấn Minh - Toán lớp 8 - Học toán với OnlineMath

a) Hai đường thẳng song song với đường thẳng a và cách đường thẳng a một khoảng là 2cm.
b) Đường tròn O B C 2 với O là trung điểm của BC
c) Đường thẳng trung trực của đoạn BC trừ trung điểm BC.

Gọi h (AH) là đường cao của \(\Delta ABC\) thì h là hằng số không đổi và cạnh đáy BC bằng a cố định .
Ta có : \(S_{ABC}=\dfrac{1}{2}BC.AH=\dfrac{1}{2}a.h\) không đổi .
Vậy diện tích tam giác ABC luôn không đồi nếu có đáy BC cố định và đỉnh A di động trên 1 đường thẳng d cố định song song với đường thẳng BC .

a) Đặt tên các điểm như hình vẽ.
Giả sử BC = a; BM = x. Ta có MN = QP = a - 2x
Áp dụng định lý Ta let ta có:
\(\frac{AQ}{AB}=\frac{QP}{BC}\Rightarrow AQ=\frac{AB.QP}{BC}=a-2x\)
\(\Rightarrow QB=AB-AQ=a-\left(a-2x\right)=2x\)
\(\Rightarrow QM=\sqrt{QB^2-BM^2}=\sqrt{4x^2-x^2}=x\sqrt{3}\)
\(\Rightarrow S_{MNPQ}=MN.QM=\left(a-2x\right).x\sqrt{3}\)
\(=-2\sqrt{3}x^2+a\sqrt{3}x\)
\(=-2\sqrt{3}\left(x^2-2.\frac{a}{4}.x+\frac{a^2}{16}\right)+\frac{a^2\sqrt{3}}{8}\)
\(=-2\sqrt{3}\left(x-\frac{a}{4}\right)^2+\frac{a^2\sqrt{3}}{8}\le\frac{a^2\sqrt{3}}{8}\)
Vậy diện tích lớn nhất của hình chữ nhật là \(\frac{a^2\sqrt{3}}{8}\) khi BM = BC/4
b) Em tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuấn Minh - Toán lớp 8 - Học toán với OnlineMath

Tam giác ABC có đáy BC cố định, diện tích không đổi nên chiều cao AH không đổi vì thế đỉnh A chuyển động trên một đường thẳng song song với BC và cách BC một khoảng bằng h không đổi.
Vậy trọng tâm G của tam giác chạy trên đường thẳng song song BC và cách BC một khoảng h/3.
Đỉnh A của các tam giác đó nằm trên đường thẳng song song với BC và cách BC một khoảng bằng 2 cm