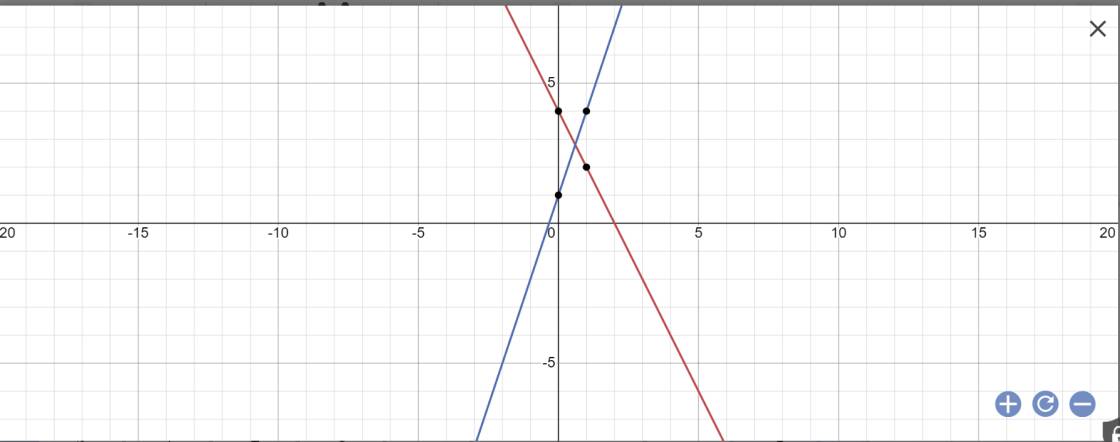
Vẽ 2 đường thẳng y=2x-4 và y=-x+2 trên cùng mặt phẳng toạ độ.Số đo(làm tròn đến độ) của góc tạo thành bởi 2 đường thẳng trên là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 12 2019
a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
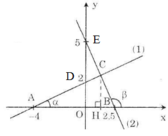
b) Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x
⇔ 0,5x + 2x = 5 – 2
⇔ 2,5.x = 3 ⇔ x = 1,2
⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
Ta có: AH = AO + OH = 4 + 1,2 = 5,2
BH = BO – OH = 2,5 – 1,2 = 1,3
CH = 2,6
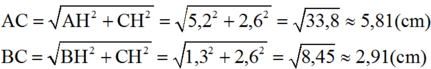
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 - 2x với tia Ox
Tam giác OEB vuông tại O nên:
19 tháng 12 2022
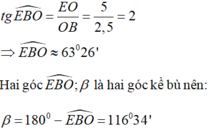
b: tan a=2
nên a=63 độ
c: Tọa độ giao của (d1) và (d2) là:
2x+3=-x+4 và y=2x+3
=>x=1/3 và y=2/3+3=8/3
Thay x=1/3 và y=8/3 vào (d3), ta được:
1/3m+m-1=8/3
=>4/3m=11/3
=>m=11/3:4/3=11/3*3/4=11/4
27 tháng 11 2016
b) Lập phương trình hoành độ giao điểm ta có;
2x - 1 = -x+2
-> 2x + x =2+1
-> 3x = 3
-> x = 1
Thay x=1 vào hàm số y = 2x - 1 ta được y= 2-1 = 1
Vậy tọa độ giao điểm M ( 1;1)
c) Thao đn TSLG có :
tanABO = \(\frac{1}{0,5}\)= 2
-> ABO ( bạn thêm kí hiệu góc vào ) \(\approx\) 63độ 26phut
Gọi \(\alpha\)là góc tạo bởi hàm số y=2x-1 và trục 0x ta có \(\alpha\)= ABO ( bạn thêm kí hiệu góc vào ) ( đối đỉnh) = 63độ 26phut
a) Xét hàm số y=2x-1 ( x\(\in\)R)
Cho x=0 -> y=-1 -> A( 0;-1)
Cho y=0 -> x= 0.5 -> B ( 0.5 : 0)
Xét hàm số y= -x+2 ( x \(\in\)R)
Cho x=0 -> y=2 -> C (0;2)
Cho y =0-> x= 2 -> D( 2;0)
vẽ đồ thị
25 tháng 12 2021
Câu 2:
Tọa độ giao điểm của hai đường thẳng là:
\(\left\{{}\begin{matrix}2x+4=-x+2\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=\dfrac{2}{3}+2=\dfrac{8}{3}\end{matrix}\right.\)
5 tháng 12 2021
c: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-1\end{matrix}\right.\)
22 tháng 12 2023
a:
b: Phương trình hoành độ giao điểm là:
4-2x=3x+1
=>-2x-3x=1-4
=>-5x=-3
=>\(x=\dfrac{3}{5}\)
Thay x=3/5 vào y=3x+1, ta được:
\(y=3\cdot\dfrac{3}{5}+1=\dfrac{9}{5}+1=\dfrac{14}{5}\)
Vậy: \(N\left(\dfrac{3}{5};\dfrac{14}{5}\right)\)
c: (d'): y=3x+1
=>a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^034'\)
12 tháng 12 2023
a:
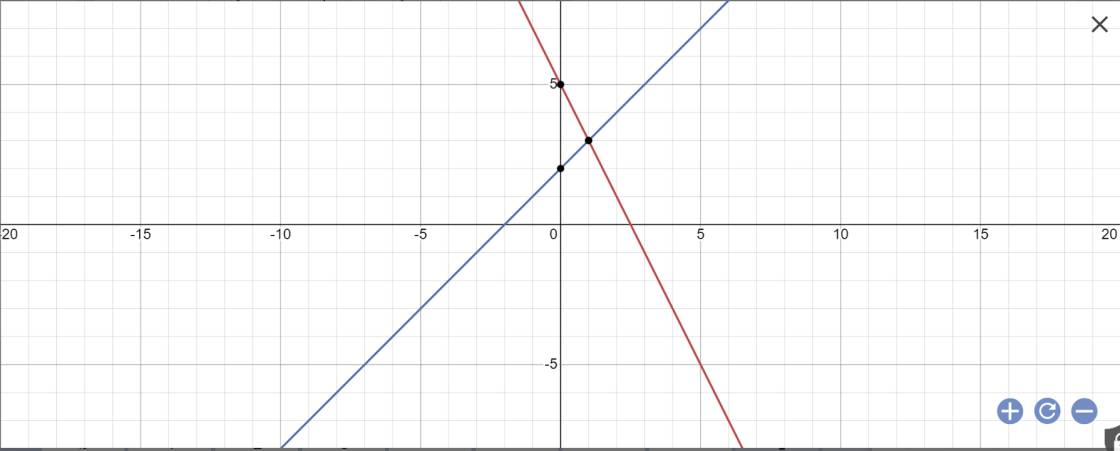
b: Phương trình hoành độ giao điểm là:
-2x+5=x+2
=>-2x-x=2-5
=>-3x=-3
=>x=1
Thay x=1 vào y=x+2, ta được;
y=1+2=3
Vậy: A(1;3)
c: Sửa đề: Tính góc tạo bởi đường thẳng y=x+2 với trục Ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
y=x+2 nên a=1
=>\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
d: Vì (d)//y=-3x-1 nên \(\left\{{}\begin{matrix}a=-3\\b\ne-1\end{matrix}\right.\)
Vậy: (d): y=-3x+b
Thay x=1 và y=3 vào (d), ta được:
\(b-3\cdot1=3\)
=>b-3=3
=>b=6(nhận)
Vậy: (d): y=-3x+6
hai đường thẳng cắt nhau tại 1 điểm trên trục hoành.
Gọi góc tạo bởi đường thẳng hs: y = -x + 2 (d1) là m và góc tạo bởi đường thẳng hs: y = 2x - 4 (d2) là n.
Và x là góc tạo bởi (d1);(d2) thì ta có: x = m - n (vì a là góc tù, b là góc nhọn).
Ta có: tan(180 - m) = 1 => 180 - m = 45 => m = 135 độ
Tan n = 2 => n = 63 độ
vì có CT: tan của góc tạo bởi đường thằng và trục Ox chính là hệ số góc a của đường thằng đó.
=>x = 72 độ