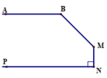
Trong hình 3 có M N ⊥ N P , A B M ^ = B M N ^ = 135 0 . Chứng minh rằng AB // NP
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tam giác \(MNP\) tam giác \(DEF\) ta có:
\(\widehat M = \widehat D\) (giả thuyết)
\(\widehat N = \widehat E\) (giả thuyết)
Do đó, \(\Delta MNP\backsim\Delta DEF\) (g.g)
Suy ra, \(\frac{{MP}}{{DF}} = \frac{{NP}}{{EF}} \Rightarrow \frac{{18}}{{24}} = \frac{{a + 2}}{{32}} \Rightarrow a + 2 = \frac{{18.32}}{{24}} = 24 \Leftrightarrow a = 24 - 2 = 22\).
Vậy \(a = 22m\).
b) Vì \(ABCD\) là hình thang nên \(AB//CD\).
Vì \(AB//CD \Rightarrow \widehat {ABM} = \widehat {MDC}\) (hai góc so le trong) và \(AB//CD \Rightarrow \widehat {BAM} = \widehat {MCD}\) (hai góc so le trong)
Xét tam giác \(AMB\) và tam giác \(CMD\) có:
\(\widehat {ABM} = \widehat {MDC}\) (chứng minh trên)
\(\widehat {BAM} = \widehat {MCD}\) (chứng minh trên)
Do đó, \(\Delta AMB\backsim\Delta CMD\) (g.g).
Ta có:
\(\frac{{AM}}{{CM}} = \frac{{BM}}{{DM}} = \frac{{AB}}{{CD}} \Leftrightarrow \frac{6}{{15}} = \frac{y}{{10}} = \frac{8}{x}\).
Ta có: \(\frac{6}{{15}} = \frac{y}{{10}} \Rightarrow y = \frac{{10.6}}{{15}} = 4\)
\(\frac{6}{{15}} = \frac{8}{x} \Rightarrow x = \frac{{8.15}}{6} = 20\).
Vậy \(x = 20;y = 4\).

a: Ta có: ΔABC=ΔDEF
nên AB=DE(1)
Ta có: ΔDEF=ΔMNP
nên DE=MN(2)
Từ (1) và (2) suy ra AB=MN

1: Xét ΔADE vuông tại D có \(\widehat{DAE}=\widehat{DEA}\left(=\widehat{EAB}\right)\)
nên ΔADE vuông cân tại D
Suy ra: AD=DE
mà DC=2DE
nên DC=2AD
hay AB=2AD
2: Ta có: ΔADE vuông cân tại D
mà DN là đường trung tuyến ứng với cạnh huyền AE
nên DN là đường cao ứng với cạnh AE

M là trung điểm của AB
N là trung điểm của AC
=> MN là đường trung bình của tam giác ABC
=> MN = BC/2
mà BP = BC/2 (P là trung điểm của BC)
=> MN = BP
mà MN // BP (MN là đường trung bình của tam giác ABC)
=> MNPB là hình bình hành
=> NI // AM
mà N là trung điểm của AC
=> I là trung điểm của CM
=> C, M, I thẳng hàng.

Gọi giao điểm của AC và BD là O
Ta có: \(OB^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Leftrightarrow\) \(4OB^2+AC^2=2\left(AB^2+BC^2\right)\)
\(\Leftrightarrow\) \(BD^2+AC^2=2\left(AB^2+BC^2\right)\) (Do \(4OB^2=\left(2OB\right)^2\) mà 2OB = BD)
\(\Leftrightarrow\) \(m^2+n^2=2\left(a^2+b^2\right)\) (đpcm)
Chúc bn học tốt!
Qua điểm M kẻ tia Mx // NP (3).
Khi đó
Xét A B M ^ + x M B ^ = 135 0 + 45 0 = 180 0 => AB // Mx (có cặp góc trong cùng phía bù nhau) (4).
Từ (3) và (4) suy ra AB // NP (đpcm).