ΔABC ~ ΔDEF theo tỉ số k 1 , ΔMNP ~ ΔDEF theo tỉ số k 2 . ΔABC ~ ΔMNP theo tỉ số nào?
A. k 1
B. k 2 k 1
C. k 1 k 2
D. k 1 k 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 7 2019
Vì ΔDEF ~ ΔABC theo tỉ số k 1 , ΔMNP ~ ΔDEF theo tỉ số k 2 nên ta có A B D E = k 1 ⇒ A B = k 1 . D E và M N D E = k 2 ⇒ M N = k 2 . D E
Từ đó ta có A B M N = D E k 1 k 2 . D E = 1 k 1 k 2 = 1 k 1 k 2
Đáp án: A
PT
1
CM
28 tháng 5 2019
Do tỉ số diện tích bằng bình phương tỉ số đồng dạng nên ta có:
NH
14 tháng 3 2023
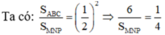
=>A
tỉ số đồng dạng bằng tỉ số chu vi, trung tuyến, phân giác, đường cao
19 tháng 2 2023
ΔABC đồng dạng vơi ΔDEF theo hệ số tỉ lệ k=5/2
=>\(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{5}{2}\)
=>\(\dfrac{C_{ABC}}{5}=\dfrac{C_{DEF}}{2}=\dfrac{1890}{7}=270\)
=>\(C_{ABC}=1350\left(cm\right);C_{DEF}=540\)
Vì ΔABC ~ ΔDEF theo tỉ số k 1 , ΔMNP ~ ΔDEF theo tỉ số k 2 nên ta có A B D E = k 1 => A B = k 1 . D E và M N D E = k 2 => M N = k 2 . D E
Từ đó ta có A B M N = k 1 . D E k 2 . D E = k 1 k 2
Đáp án: D