PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 9
ΔABC~ΔMNP
=>\(\hat{B}=\hat{N};\hat{BAC}=\hat{NMP}\)
ta có: \(\hat{BAD}=\frac12\cdot\hat{BAC}\) (AD là phân giác của góc BAC)
\(\hat{NME}=\frac12\cdot\hat{NMP}\) (ME là phân giác của góc NMP)
mà \(\hat{BAC}=\hat{NMP}\)
nên \(\hat{BAD}=\hat{NME}\)
Xét ΔBAD và ΔNME có
\(\hat{BAD}=\hat{NME}\)
\(\hat{B}=\hat{N}\)
Do đó: ΔBAD~ΔNME
=>\(\frac{AD}{ME}=\frac{BA}{MN}=k\)
CM
10 tháng 7 2019
Vì ΔDEF ~ ΔABC theo tỉ số k 1 , ΔMNP ~ ΔDEF theo tỉ số k 2 nên ta có A B D E = k 1 ⇒ A B = k 1 . D E và M N D E = k 2 ⇒ M N = k 2 . D E
Từ đó ta có A B M N = D E k 1 k 2 . D E = 1 k 1 k 2 = 1 k 1 k 2
Đáp án: A
CM
3 tháng 6 2019
Vì ΔABC ~ ΔDEF theo tỉ số k 1 , ΔMNP ~ ΔDEF theo tỉ số k 2 nên ta có A B D E = k 1 => A B = k 1 . D E và M N D E = k 2 => M N = k 2 . D E
Từ đó ta có A B M N = k 1 . D E k 2 . D E = k 1 k 2
Đáp án: D
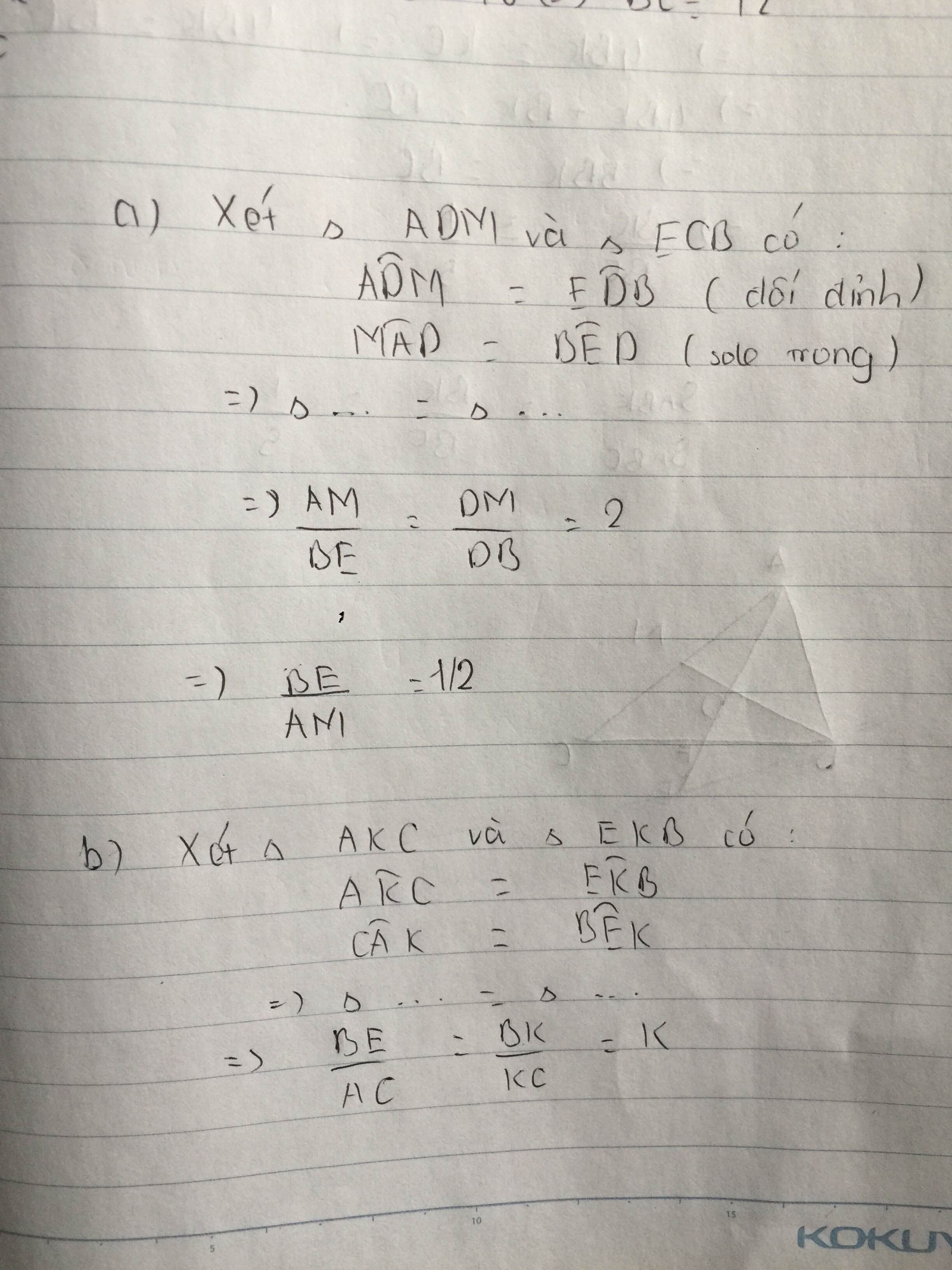
Do tỉ số diện tích bằng bình phương tỉ số đồng dạng nên ta có: