Cho x bông hồng trắng và y bông hồng nhung khác nhau. Cho biết x, y là nghiệm của hệ bất phương trình C x x - 2 + C y + 3 2 + 9 2 < 19 2 A x 1 P y - 1 = 720 . Tính xác suất để lấy được 5 bông hồng trong đó có ít nhất 3 bông hồng nhung
A. 193 442
B. 319 442
C. 139 442
D. 391 442


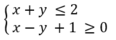 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.
Trước hết ta giải hệ bất phương trình để tìm x, y
Phương trình trong hệ cho ta
y - 1 ! = 720 ⇔ y - 1 ! = 6 ! ⇔ y - 1 = 6 ⇔ y = 7
Thay y = 7 vào bất phương trình trong hệ ta được: C x x - 2 + C 10 2 + 9 2 < 19 2 A x 1
Với điều kiện x ≥ 2 , x ∈ N , bất phương trình tương đương với:
x ! 2 ! x - 2 ! + 45 + 9 2 < 19 2 x ⇔ x x - 1 2 + 45 + 9 2 < 19 2 x
⇔ x 2 - 20 x + 99 < 0 ⇔ 9 < x < 11 Vì x ∈ N nên x = 10
Như vậy ta có 10 bông hồng trắng và 7 bông hồng nhung. Để lấy được ít nhất 3 bông hồng nhung trong 5 bông hồng ta có các trường hợp sau:
Trường hợp 1: 3 bông hồng nhung, 2 bông hồng trắng có C 7 1 . C 10 2 = 1575 cách
Trường hợp 2: 4 bông hồng nhung, 1 bông hồng trắng có C 7 4 . C 10 1 = 350 cách
Trường hợp 3: 5 bông hồng nhung có C 7 5 = 21 cách
Suy ra có tất cả 1575 + 350 + 21 = 1946 cách.
Số cách lấy ra 5 bông hồng bất kì là C 17 5 = 6188 .
Vậy xác suất cần tìm là P = 1946 6188 = 139 442
Đáp án C