Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Số cách lấy 3 bông hồng bất kì: 
Số cách lấy 3 bông hồng chỉ có một màu: 
Số cách lấy 3 bông hồng có đúng hai màu: 
Vậy số cách chọn thỏa yêu cầu bài toán là:.2300-211-1529=560
Chọn A.
Đáp án : A
Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 7 cách chọn hoa hồng trắng.
Có 5 cách chọn hoa hồng đỏ.
Có 6 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 7.5.6=210 cách.
Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 5 cách chọn hoa hồng trắng.
Có 6 cách chọn hoa hồng đỏ.
Có 7 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 5.6.7= 210 cách.
Chọn đáp án B.
Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 5 cách chọn hoa hồng trắng.
Có 6 cách chọn hoa hồng đỏ.
Có 7 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 5.6.7 = 210 cách.
Chọn đáp án B.
Không gian mẫu: \(C_{16}^3\)
a. Số cách chọn 3 bông cùng loại: \(C_5^3+C_7^3+C_4^3=...\)
Xác suất: \(P=\dfrac{C_5^3+C_7^3+C_4^3}{C_{16}^3}=...\)
b. Số cách chọn không có bông nhung nào: \(C_{11}^3\)
Số cách chọn có ít nhất 1 bông nhung: \(C_{16}^3-C_{11}^3\)
Xác suát: \(P=\dfrac{C_{16}^3-C_{11}^3}{C_{16}^3}\)
Chọn ngẫu nhiên 7 bông hoa tứ 3 bó ta có \(C^7_{21}\) cách.
Chọn 7 bông hoa trong đó số bông hoa hồng bằng số bông hoa ly xảy ra các trường hợp sau :
- Trường hợp 1 : Chọn 7 bông hoa trong đó có 1 bông hoa hồng, 1 bông hoa ly và 5 bông hoa huệ có \(C^1_8C^1_7C^5_6\) cách.
- Trường hợp 2 : Chọn 7 bông hoa trong đó có 2 bông hoa hồng, 2 bông hoa ly và 3 bông hoa huệ có \(C^2_8C^2_7C^3_6\) cách.
- Trường hợp 3 : Chọn 7 bông hoa trong đó có 3 bông hoa hồng, 3 bông hoa ly và 1 bông hoa huệ có \(C^3_8C^3_7C^1_6\) cách.
Từ các trường hợp trên ta có \(C^1_8C^1_7C^5_6+C^2_8C^2_7C^3_6+C^3_8C^3_7C^1_6=12306\) cách chọn 7 bông hoa trong đó số bông hoa hồng bằng số bông hoa ly.
Xác suất cần tính là : \(p=\frac{2015}{19380}\approx0.106\)
Đáp án A.
Hướng dẫn giải:
Số cách lấy 3 bông hồng bất kỳ: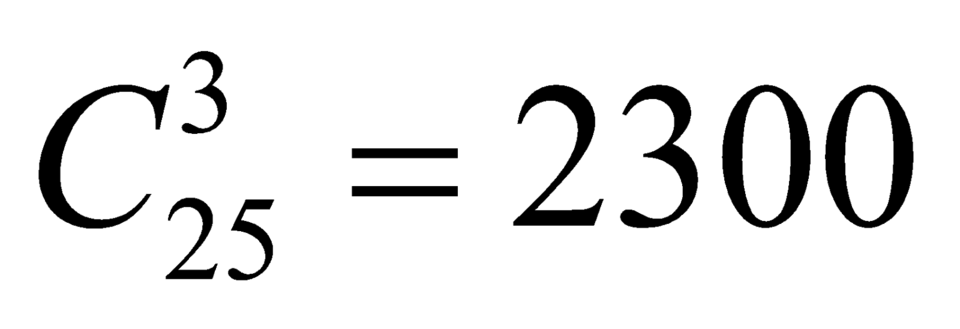
+ Số cách lấy 3 bông hồng chỉ có một màu:
+ Số cách lấy 3 bông hồng có đúng hai màu:
Vậy số cách chọn thoả yêu cầu bài toán là: