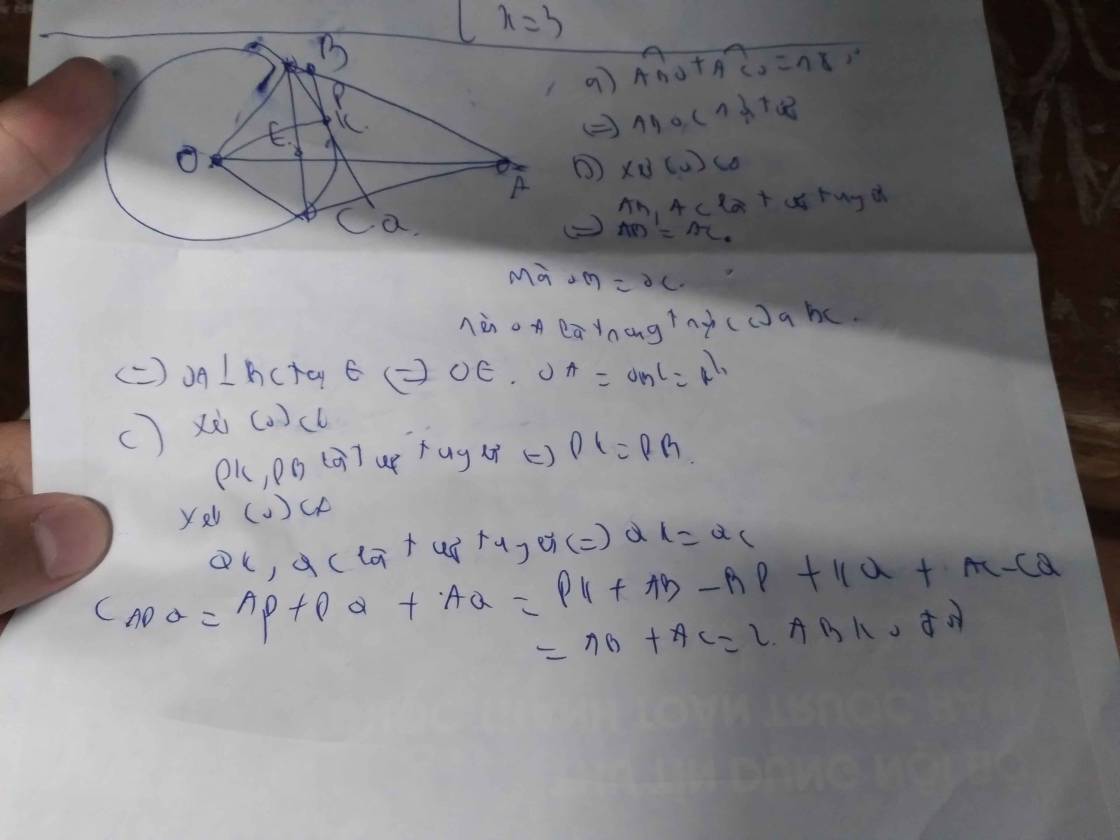
cho đường tròn (o:r) điểm a nằm bên ngoài đường tròn kẻ tiếp tuyến ab ac (b,c là 2 tiếp điểm) a)CMR:bốn điểm A,B,O,C cùng nằm trên một đường tròn b)Gọi E là giao điểm của BC và OA . CMR:OE*OA=R bình phương c)Trên cung nhỏ BC của đường tròn (o;r) lấy điểm K bất kỳ (khác B,C) .Tiếp tuyến K của đường tròn (o;r) cắt AB và AC tại P,Q.CMR: Chu vi tam giác APQ không đổi khi K di chuyển trên cung BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc với BC
=>OH*OA=OB^2=R^2
b: góc ABM=góc ACM
góc HBM=90 độ-góc OMB=90 độ-góc OBM=góc ABM
=>BM là phân giác của góc ABH

a) Xét (O):
D đối xứng với B qua O (gt).
\(\Rightarrow\) O là trung điểm của BD.
\(\Rightarrow\) BD là đường kính của (O).
Xét (O):
BD là đường kính của (O) (cmt).
\(E\in\left(O\right)\left(gt\right).\)
\(\Rightarrow\widehat{BED}=90^o.\)
Xét (O):
AB là tiếp tuyến (gt).
\(\Rightarrow BD\perp AB\) (Tính chất tiếp tuyến).
\(\Rightarrow\widehat{ABD}=90^o.\)
Xét \(\Delta ADB\) và \(\Delta BDE:\)
\(\widehat{ABD}=\widehat{BED}\left(=90^o\right).\\ \widehat{ADB}chung.\)
\(\Rightarrow\dfrac{BD}{DE}=\dfrac{AB}{BE}\) (2 cạnh tương ứng tỉ lệ).
\(\Rightarrow BD.BE=BA.DE.\)

a/
Hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì đường thẳng nối điểm đó với tâm đường tròn vuông góc và chia đôi dây cung nối 2 tiếp điểm
\(\Rightarrow AO\perp BC\) (đpcm)
\(\Rightarrow BH=CH=\dfrac{BC}{2}\)
b/
Ta có
B và C cùng nhìn AO dưới 1 góc vuông nên B và C cùng nằm trên đường tròn đường kính AO => A; O; B; C cùng nằm trên 1 đường tròn
c/
Ta có sđ cung IB = sđ cung IC ( Hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì chia đôi cung chắn bởi hai tiếp điểm)
Xét tg vuông IBK và tg vuông IBH có
\(sđ\widehat{IBK}=\dfrac{1}{2}sđ\) cung IB (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{IBH}=\dfrac{1}{2}sđ\) cung IC (góc nội tiếp đường tròn)
Mà sđ cung IB = sđ cung IC (cmt)
\(\Rightarrow\widehat{IBK}=\widehat{IBH}\)
cạnh huyền IB chung
\(\Rightarrow\Delta IBK=\Delta IBH\) (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
\(\Rightarrow IK=IH\) (đpcm)
d/ Mình nghĩ mãi chỉ có 1 cách nhưng hơi dài mình nói cách làm thôi nhé
Vận dụng các hệ thức lượng trong tg vuông và t/c của hai tiếp tuyến cùng xp từ 1 điểm Sẽ tính được AB=AC;BC; AH từ đó tính được diện tích tg ABC
Vận dụng công thức \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin\widehat{KAE}\) từ đó tính được \(\sin\widehat{KAE}\)
Tương tự ta cũng tính được \(\sin\widehat{AKE}\)
Vận dụng định lý hàm sin
\(\dfrac{KE}{\sin\widehat{KAE}}=\dfrac{AE}{\sin\widehat{AKE}}\Rightarrow\dfrac{KM+EM}{\sin\widehat{KAE}}=\dfrac{AC+EC}{\sin\widehat{AKE}}\)
Mà KM=KB (hai tiếp tuyến cùng xp từ 1 điểm)
tg IBK = tg IBH (cmt) => KB=BH
=> KB=KM=BH Mà BH tính được AC tính được; EM=EC (2 tiếp tuyến cùng xp từ 1 điểm)
Giải PT để tìm EC Từ đó tính được AK; KE; AE
\(\Rightarrow S_{AKE}=\dfrac{1}{2}\left(AK+KE+AE\right).R\)
Bạn tự làm nhé
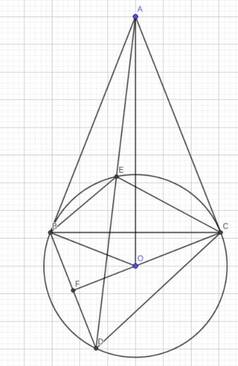
a ) Ta có : AB , AC là tiếp tuyến của (O)
nội tiếp
b ) Vì AB là tiếp tuyến của (O)
c ) Ta có :