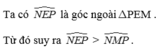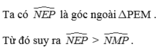Cho tam giác MNP, E là một điểm trên cạnh MN. Chứng minh: NEP>NMP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
28 tháng 8 2021
Bạn vẽ hình vào nhé
a) Xét tg DEM có ME=DE( gt)
DI = IE( gt)
=> DI là dg tb tg DEM => DI//MD; DI =1/2 MD
Xét tg DEN có DF=FN(gt)
DI = IE(gt)
=> FI là dg tb tg DEN=> FI//EN ; FI=1/2EN
Mà NE = MP(gt)=> 1/2NE=1/2MP=>DI =FI=> tg DFI cân tại I
Bạn sửa lại b thành I nhé( trong đề bài ý)
b) Ta có : ID// MD( ID là dg tb tg DEM)
=> IDN=DME. (1)
Ta có FI// EN( FI là dg tb tg DEN)=> IFD=FDN(slt)
Mà IDF+FDN= IDN. (2)
Ta lại có IFD=IDF( tg DIF cân tại I) (3)
=> Từ (1) (2) (3) suy ra MNP= 2 IDF
14 tháng 8 2023
a: Xét ΔAMN và ΔAPE có
AN=AE
MN=PE
AM=AP
=>ΔAMN=ΔAPE
b: ΔAMN=ΔAPE
=>góc NMA=góc EAP
=>góc NMA=góc AMP
=>MA là phân giác của góc NMP
2 tháng 1 2022
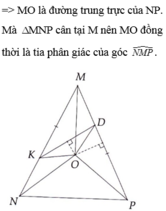
b: Xét ΔMND và ΔMPD có
MN=MP
ND=PD
MD chung
Do đó: ΔMND=ΔMPD
10 tháng 5 2023
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: ΔMNP vuông tại M co MH vuông góc NP
nên MH^2=HN*HP