Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác HMN và tam giác MNP:
Góc B chung.
Góc MHN = Góc NMP (cùng = 90o).
=> Tam giác HMN \(\sim\) Tam giác MNP (g - g).
b) Xét tam giác MNP vuông tại M, MH là đường cao:
=> MH2 = NH . PH (Hệ thức lượng trong tam giác vuông).
c) Xét tam giác NFH và tam giác MEH:
Góc FNH = Góc EMH (cùng phụ với góc MPN).
Góc NHF = Góc MHE (cùng phụ với góc MHF).
=> Tam giác NFH \(\sim\) Tam giác MEH (g - g).
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
\(\widehat{N}\) chung
Do đó: ΔHNM\(\sim\)ΔMNP
b: Xét ΔMNP vuông tại M có MH là đường cao
nên \(MH^2=NH\cdot PH\)

a,Xét tam giác HNM và tam giác MNP
Góc N chung
Góc NMP = góc NHM
=> Tam giác HNM đồng dạng tam giác MNP (gg)
b, Chứng minh đc tam giác MNP đồng dạng tam giác HMP(gg)
=> Tam giác HNM đồng dạng tam giác HMP
=>\(\frac{NH}{MH}\)=\(\frac{MH}{PH}\)
<=> NH.PH=MH2
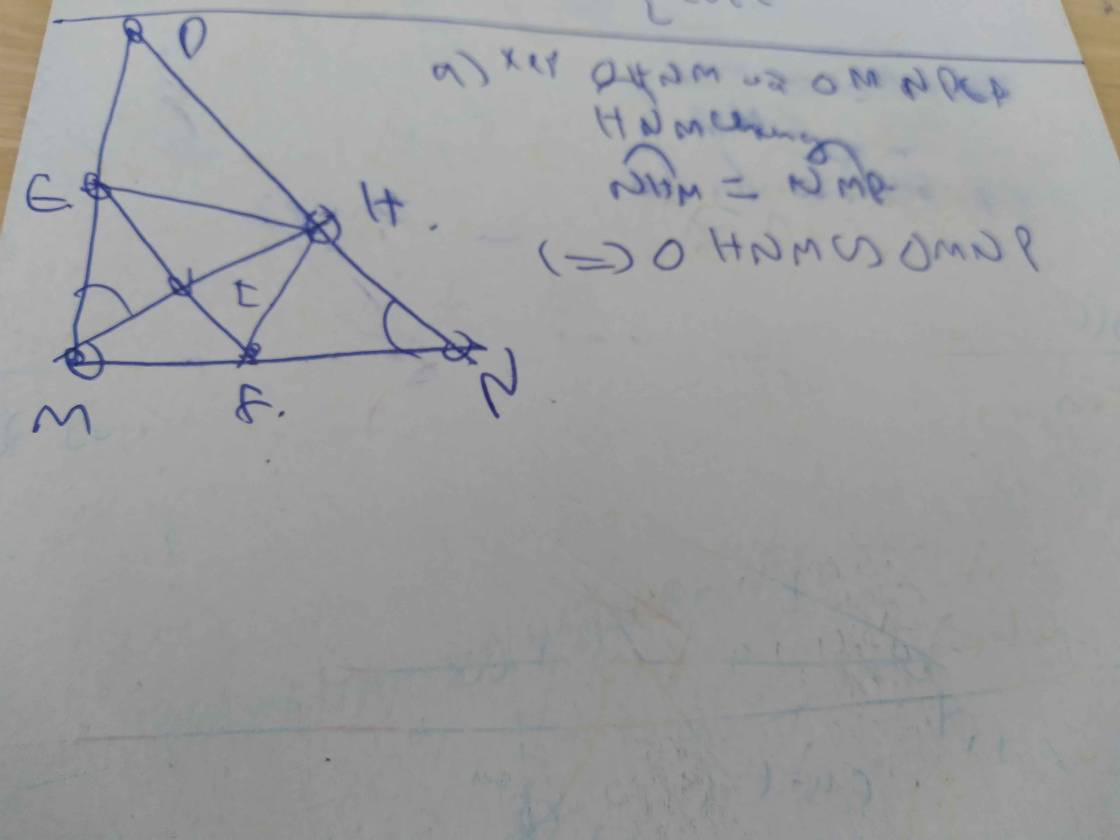
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: ΔMNP vuông tại M co MH vuông góc NP
nên MH^2=HN*HP