Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu a ghi sai : góc nko mới đúng
A, ta có
Tam giác mnp cân tại m
Suy ra Mn=mp
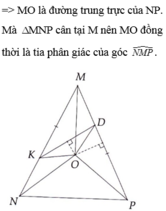
Vì mo là đường trung trực của kd nên mo vuông góc với kd ( định nghĩa)
Vì mn = mp
Kn = dp
Mà mn= mk+kn
Mp=md+dp
Suy ra mk=md ( tính chất bắc cầu)
Xét tam giác mko và tam giác mdo vuông tại o
Mk=md ( cmt)
Mo chung
Suy ra tam giác mko = tam giác mdo ( ch-cgv)
Suy ra góc mko = góc mdo
Mà góc nko + mko = 180°
Odp + mdo = 180°
Suy ra okn = góc odp . Đpcm
B, vì theo đề bài
Mo là đường trung trực của kd
Mà kd cắt đường trung trực của mp
Suy ra m thuộc đường trung trực của mp. Đpcm
C,
Theo câu a ta có
Tam giác mko = tam giác mdo
Suy ra góc kmo = góc dmo ( cạnh tương ứng)
Suy ra mo là tia phân giác của góc kmd .( định nghĩa) đpcm

Chỉ còn vài tiếng nữa là mình nộp bài rồi, mong các bạn dành ra ít thời gian để giúp đỡ mình. Mình sẽ tích đúng cho các bạn, mình cảm ơn trước!!!!

a/ Xét \(\Delta ABD\) và \(\Delta KBD\)
AB=BK (gt); BD chung
\(\widehat{ABD}=\widehat{KBD}\) (gt)
\(\Rightarrow\Delta ABD=\Delta KBD\left(c.g.c\right)\Rightarrow AD=DK\)
b/
\(\Delta ABD=\Delta KBD\Rightarrow\widehat{BAC}=\widehat{BKD}=90^o\Rightarrow DK\perp BC\)
\(AH\perp BC\left(gt\right)\)
=> AH//DK (cùng vuông góc với BC)
c/
Gọi M' là giao của BD với CE. Xét \(\Delta BCE\) có
\(EK\perp BC,CA\perp BE\)=> D là trực tâm của \(\Delta BCE\Rightarrow BM\perp CE\) (trong tam giác 3 đường cao đồng quy tại 1 điểm gọi là trực tâm của tam giác)
Mà BM là phân giác của \(\widehat{ABC}\Rightarrow\Delta BCE\) cân tại B (trong tam giác đường cao đồng thời là đường phân giác thì tg đó là tg cân)
=> BM' là đường trung tuyến (trong tg cân đường cao xp từ đỉnh đồng thời là đường trung tuyến của tam giác)
=> M' là trung điểm của CE, mà M cũng là trung điểm của CE => M trùng M' => B, D, M thẳng hàng