x2+2x+1-16y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính 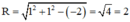
b) 16x2 + 16y2 + 16x – 8y –11 = 0
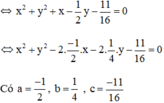
⇒ Đường tròn có tâm 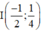 , bán kính
, bán kính 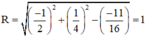
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính 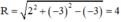
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
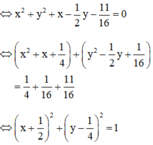
Vậy đường tròn có tâm 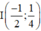 và bán kính R = 1.
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.

b: \(8x^2-48x+6xy-36y\)
\(=8x\left(x-6\right)+6y\left(x-6\right)\)
\(=2\left(x-6\right)\left(4x+3y\right)\)
d: \(a^2-2ab+b^2-4\)
\(=\left(a-b\right)^2-4\)
\(=\left(a-b-2\right)\left(a-b+2\right)\)

a) \(a^2b-4ab^2\)
\(=ab\left(a-4b\right)\)
b) \(x^8+4y^4\)
\(=\left(x^4\right)^2+\left(2y^2\right)^2\)
\(=\left(x^4-2y^2\right)\left(x^4+2y^2\right)\)
c) \(x^2-10x-16y^2+25\)
\(=\left(x^2-10x+25\right)-16y^2\)
\(=\left(x-5\right)^2-\left(4y\right)^2\)
\(=\left[\left(x-5\right)+4y\right]\left[\left(x-5\right)-4y\right]\)
\(=\left(x-5+4y\right)\left(x-5-4y\right)\)

Lời giải:
a)
Áp dụng BĐT Bunhiacopxky:
\((y-2x)^2\leq (16y^2+36x^2)(\frac{1}{16}+\frac{1}{9})=9.\frac{25}{144}\)
\(\Rightarrow \frac{-5}{4}\leq y-2x\leq \frac{5}{4}\Rightarrow \frac{15}{4}\leq y-2x+5\leq \frac{25}{4}\)
Vậy $A_{\min}=\frac{15}{4}$ và $A_{\max}=\frac{25}{4}$
b)
Áp dụng BĐT Bunhiacopxky:
\((2x-y)^2\leq (\frac{x^2}{4}+\frac{y^2}{9})(16+9)=25\)
\(\Rightarrow -5\leq 2x-y\leq 5\Leftrightarrow -7\leq 2x-y-2\leq 3\)
Vậy $B_{min}=-7; B_{\max}=3$

D = ( 15 x y 2 + 18 x y 3 + 16 y 2 ) : 6 y 2 – 7 x 4 y 3 : x 4 y ⇔ D = 15 x y 2 : ( 6 y 2 ) + 18 x y 3 : ( 6 y 2 ) + 16 y 2 : ( 6 y 2 ) – 7 x 4 y 3 : x 4 y ⇔ D = 5 2 x + 3 x y + 8 3 - 7 y 2
Tại x = 2 3 và y = 1 ta có
D = 5 2 . 2 3 + 3 . 2 3 . 1 + 8 3 - 7 . 1 2 = 5 3 + 2 + 8 3 - 7 = 13 3 - 5 = - 2 3
Đáp án cần chọn là: D

Câu 2:
a: SỬa đề: \(x^2-y^2+6x+9\)
\(=\left(x^2+6x+9\right)-y^2\)
\(=\left(x+3+y\right)\left(x+3-y\right)\)
b: \(=4x^2+4x+1-16y^2\)
\(=\left(2x+1\right)^2-16y^2\)
\(=\left(2x+1+4y\right)\left(2x+1-4y\right)\)
c: \(=6x^2+3xy+4xy+2y^2\)
\(=3x\left(x+2y\right)+2y\left(x+2y\right)\)
=(x+2y)(3x+2y)

\(x^2+2x+1-16y^2\)
\(=\left(x+1\right)^2-\left(4y\right)^2\)
\(=\left(x+1-4y\right)\left(x+1+4y\right)\)