cho AB //CD tính x,y,z a B z A x c C D 42 độ 75 độ ...
Đọc tiếp
cho AB //CD tính x,y,z
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 4 2020
a) Vì x,y,z>0 nên a,b,c>0 (1)
Ta có: a+b-c=x+y+y+z-z-x=2y>0
=> a+b>c. Tương tự ta có b+c>a, c+a>b (2)
Từ (1) và (2) => Tồn tại tam giác mà các cạnh của nó có độ dài 3 cạnh là a,b,c
b) Vì a,b,c là độ dài 3 cạnh của 1 tam giác nên ta có a+b>c hay x+y+y+z>z+x => y>0
Tương tự: z,x>0
Vậy có các số dương x,y,z tm
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
(C) là đường tròn tâm \(I\left(2;-3\right)\) bán kính \(R=5\)
\(\overrightarrow{DI}=\left(1;-4\right)\Rightarrow ID=\sqrt{17}< R\Rightarrow\) D là 1 điểm thuộc miền trong đường tròn
Gọi H là hình chiếu vuông góc của I lên \(\Delta\Rightarrow\) H là trung điểm AB
Theo định lý Pitago: \(AH^2=IA^2-IH^2=R^2-IH^2\Leftrightarrow\dfrac{1}{4}AB^2=25-IH^2\)
\(\Rightarrow AB\) đạt min khi và chỉ khi IH đạt max
Mặt khác trong tam giác vuông IDH, theo định lý đường xiên-đường vuông góc ta luôn có:
\(IH\le ID\Rightarrow IH_{max}=ID\) khi H trùng D \(\Leftrightarrow\Delta\perp ID\)
\(\Rightarrow\) đường thẳng \(\Delta\) nhận (1;-4) là 1 vtpt
Phương trình \(\Delta\):
\(1\left(x-1\right)-4\left(y-1\right)=0\Leftrightarrow x-4y+3=0\)
\(\Rightarrow\left\{{}\begin{matrix}b=-4\\c=3\end{matrix}\right.\)
28 tháng 8 2019
2
a
\(x+y+z=0\)
\(\Rightarrow x+y=-z\)
\(\Rightarrow\left(x+y\right)^3=\left(-z\right)^3\)
\(\Rightarrow x^3+y^3+3x^2y+3xy^2=-z^3\)
\(\Rightarrow x^3+y^3+z^3=3xy\left(x+y\right)=3xyz\)
b
Đặt \(a-b=x;b-c=y;c-a=z\Rightarrow x+y+z=0\)
Ta có bài toán mới:Cho \(x+y+z=0\).Phân tích đa thức thành nhân tử:\(x^3+y^3+z^3\)
Áp dụng kết quả câu a ta được:
\(\left(a-b\right)^3+\left(b-c\right)^3+\left(c-a\right)^3=3\left(a-b\right)\left(b-c\right)\left(c-a\right)\)
1 tháng 2 2017
\(A=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc^2}{ac+abc^2+abc}\)
\(=\frac{a}{a\left(bc+b+1\right)}+\frac{b}{bc+b+1}+\frac{abc^2}{ac\left(bc+b+1\right)}\)
\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+b+1}\)
\(=\frac{bc+b+1}{bc+b+1}=1\)
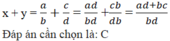
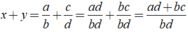
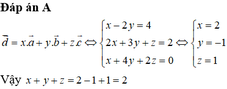
y đâu bn