Tìm x
3x2 + 7x = 10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
6 tháng 2 2019
TXĐ: D = (− ∞ ; − 6 ) ∪ ( 6 ; + ∞ )
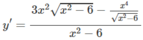
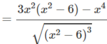
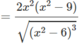
Bảng biến thiên:
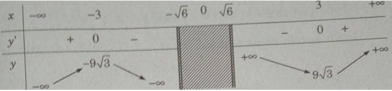
Từ đó ta thấy hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x = -3 và y CT = y(3) = 9 3 ; y CD = y(−3) = −9 3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 11 2023
a,A = \(\dfrac{3x^2+6xy}{6x^2}\) (đk \(x\) ≠ 0)
A = \(\dfrac{3x.\left(x+2y\right)}{6x^2}\)
A = \(\dfrac{x+2y}{2x}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 11 2023
b,B = \(\dfrac{2x^2-x^3}{x^2-4}\) (đk \(x\)2 - 4 ≠ 0 ⇒ \(x\) ≠ \(\pm\) 2)
B = \(\dfrac{x^2\left(2-x\right)}{\left(x+2\right)\left(x-2\right)}\)
B = \(\dfrac{-x^2.\left(x-2\right)}{\left(x+2\right).\left(x-2\right)}\)
B = \(\dfrac{-x^2}{x+2}\)
PT
1
CM
19 tháng 1 2018
TXĐ: (- ∞ ; 6 ) ∪ ( 6 ; + ∞ )
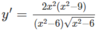
y’ = 0 ⇔ x = 3 hoặc x = -3
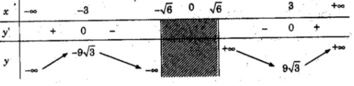
Vậy hàm số đồng biến trên các khoảng (- ∞ ; -3), (3; + ∞ ), nghịch biến trên các khoảng (-3; − 6 − 6 ), ( 6 ; 3).
PT
1
CM
5 tháng 8 2018
Chọn B
Ta có: f ' x = 0 ⇔ x 3 x 2 - 1 = 0
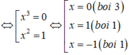
Vậy hàm số đã cho có 3 điểm cực trị
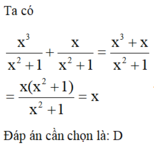
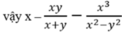
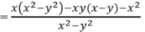
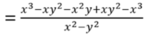
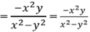
\(3x^2+7x=10\)
\(3x^2+7x-10=0\)
\(\left(x-1\right)\left(3x+10\right)=0\)
\(\orbr{\begin{cases}x-1=0\\3x+10=0\end{cases}\Rightarrow\orbr{\begin{cases}x=1\\x=-\frac{10}{3}\end{cases}}}\)
\(3x^2+7x=10\)
\(\Leftrightarrow3x^2+7x-10=0\)
\(\Leftrightarrow3x^2-3x+10x-10=0\)
\(\Leftrightarrow3x\left(x-1\right)+10\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x+10\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\3x+10=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\3x=-10\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-\frac{10}{3}\end{cases}}\)
Vậy \(x=1\)hoặc \(x=-\frac{10}{3}\)