Chứng minh rằng: B = 6b - b2 - 10 < 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
12 tháng 1 2022
\(\dfrac{a}{b}=\dfrac{b}{c}\Rightarrow ac=b^2\)
\(\dfrac{a^2+b^2}{b^2+c^2}=\dfrac{a^2+ac}{ac+c^2}=\dfrac{a\left(a+c\right)}{c\left(a+c\right)}=\dfrac{a}{c}\)
PT
1
CM
29 tháng 12 2017
Xét a + b 8 với mọi a,b ≥ 0 ta có:
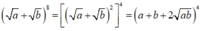
Áp dụng bất đẳng Cô-si cho hai số dương a + b và 2 a b ta được:
NT
2
CM
13 tháng 10 2017
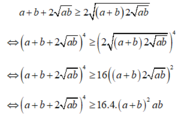
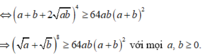
c 2 x 2 + a 2 - b 2 - c 2 x + b 2 = 0.
Δ = a 2 - b 2 - c 2 2 - 4 b 2 c 2
= a 2 - b 2 - c 2 2 - 2 b c 2
= ( a 2 - b 2 - c 2 + 2bc)( a 2 - b 2 - c 2 - 2bc)
= [ a 2 - b - c 2 ][ a 2 - b + c 2 ]
= (a + b – c)(a – b + c)(a + b + c)(a – b – c)
Vì a; b; c là độ dài ba cạnh của một tam giác, dựa vào tính chất bất đẳng thức tam giác, ta có: |b – c| < a < b + c.
Do đó a + b + c > 0; a + b – c > 0; a – b + c > 0 còn a – b – c < 0.
Suy ra Δ < 0. Vậy phương trình đã cho vô nghiệm.
HN
1
20 tháng 8 2023
Ta có :
\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab-2bc-2ac\)
mà theo đề bài \(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-\left(ab+bc+ac\right)=0\)
mà \(-\left(ab+bc+ac\right)\le0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow dpcm\)
R và a,b,c 
0 thoả mãn b2 = ac. Chứng minh rằng:
= 
11 tháng 12 2020
1/a+1/b+1/c=0
=>(ab+ac+bc)/abc=0
=> ab+ac+bc=0
(a+b+c)^2=a^2+b^2+c^2+2(ab+ac+bc)=0
=> a^2+b^2+c^2=0
Bạn xem lại đề nhé.
Ta có :
\(B=6b-b^2-10\)
\(\Leftrightarrow B=-b^2+6b-9-1\)
\(\Leftrightarrow B=-\left(b^2-6b+9\right)-1\)
\(\Leftrightarrow B=-\left(b-3\right)^2-1< 0\)( luôn đúng với mọi b )
Vậy ..........