Câu 1: Cho các số a, b, c, d, e lần lượt là số tuổi của năm người, trong đó a bằng 2 lần b, bằng 3 lần c, bằng 4 lần d và bằng 6 lần e. Tìm giá trị nhỏ nhất có thể có của a +b + c +d + e.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
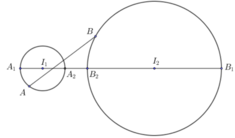
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8

Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk

a: f(x) có ĐKXĐ là 6-x>=0
=>x<=6
=>\(A=(-\infty;6]\)
g(x) có ĐKXĐ: là 2x+1<>0
=>\(x< >-\dfrac{1}{2}\)
=>\(B=R\backslash\left\{-\dfrac{1}{2}\right\}\)
\(A\cap B=(-\infty;6]\cap\left(R\backslash\left\{-\dfrac{1}{2}\right\}\right)\)
\(=(-\infty;6]\backslash\left\{\dfrac{1}{2}\right\}\)
\(A\cup B=R\)
\(A\text{B}=(-\infty;6]\backslash\left(R\backslash\left\{-\dfrac{1}{2}\right\}\right)=\left\{-\dfrac{1}{2}\right\}\)
\(B\backslash A=\left(6;+\infty\right)\)

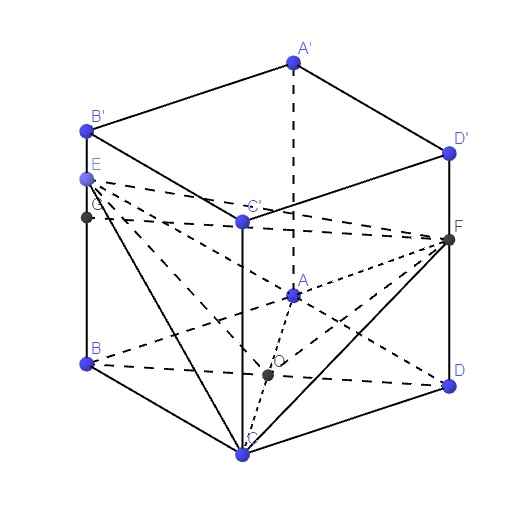
Gọi O là giao điểm AC và BD
Do lăng trụ đều \(\Rightarrow AC\perp\left(BDD'B'\right)\Rightarrow AC\perp\left(EOF\right)\)
\(V_{ACEF}=V_{AOEF}+V_{COEF}=2V_{AOEF}=\dfrac{2}{3}AO.S_{OEF}=\dfrac{a\sqrt{2}}{3}.S_{OEF}\)
Đặt \(BE=x;\) \(DF=y\), trên BB' lấy G sao cho \(BG=DF=y\)
\(\Rightarrow FG=BD=a\sqrt{2}\) và \(EG=\left|x-y\right|\)
\(\Rightarrow EF=\sqrt{EG^2+FG^2}=\sqrt{2a^2+\left(x-y\right)^2}\)
\(OE=\sqrt{OB^2+BE^2}=\sqrt{\dfrac{a^2}{2}+x^2}\) ; \(OF=\sqrt{OD^2+DF^2}=\sqrt{\dfrac{a^2}{2}+y^2}\)
Do \(\left(EAC\right)\perp\left(FAC\right)\Rightarrow OE\perp OF\)
\(\Rightarrow OE^2+OF^2=EF^2\)
\(\Rightarrow a^2+x^2+y^2=2a^2+\left(x-y\right)^2\Rightarrow xy=\dfrac{a^2}{2}\)
\(S_{OEF}=\dfrac{1}{2}OE.OF=\dfrac{1}{2}\sqrt{\left(\dfrac{a^2}{2}+x^2\right)\left(\dfrac{a^2}{2}+y^2\right)}=\dfrac{1}{2}\sqrt{\dfrac{a^4}{4}+\left(xy\right)^2+\dfrac{a^2}{2}\left(x^2+y^2\right)}\)
\(=\dfrac{1}{2}\sqrt{\dfrac{a^4}{2}+\dfrac{a^2}{2}\left(x^2+y^2\right)}\ge\dfrac{1}{2}\sqrt{\dfrac{a^4}{2}+\dfrac{a^2}{2}.2xy}=\dfrac{1}{2}\sqrt{\dfrac{a^4}{2}+a^2.\dfrac{a^2}{2}}=\dfrac{a^2}{2}\)
\(\Rightarrow V_{ACEF}\ge\dfrac{a\sqrt{2}}{3}.\dfrac{a^2}{2}=\dfrac{a^3\sqrt{2}}{6}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{a\sqrt{2}}{2}\)

Đáp án D
I đúng, vì 2 gen này được nhân đôi khi NST nhân đôi
II sai, phiên mã dựa vào nhu cầu của tế bào với sản phầm của 2 gen đó
III đúng
IV đúng

Đáp án A
Có 3 phát biểu đúng, đó là I, III và IV. → Đáp án A.
- Các gen trong nhân tế bào có số lần nhân đôi bằng nhau. → I đúng.
- Các gen khác nhau thì thường có số lần phiên mã khác nhau. → II sai.
- Đột biến thể một thì chỉ có 1 NST nên các gen ở trên NST số 2 đều chỉ có 1 bản sao. → III đúng.
- Chất 5BU gây đột biến thay thế cặp A-T bằng cặp G-X. → IV đúng

Đáp án A
Có 3 phát biểu đúng, đó là I, III và IV. → Đáp án A.
- Các gen trong nhân tế bào có số lần nhân đôi bằng nhau. → I đúng.
- Các gen khác nhau thì thường có số lần phiên mã khác nhau. → II sai.
- Đột biến thể một thì chỉ có 1 NST nên các gen ở trên NST số 2 đều chỉ có 1 bản sao. → III đúng.
- Chất 5BU gây đột biến thay thế cặp A-T bằng cặp G-X. → IV đúng.
Vì a, b, c, d, e là số tuổi của 5 người
\(\Rightarrow a,b,c,d,e\inℕ^∗\)
Vì \(a=2b=3c=4d=6e\)( giả thiết )
\(\Rightarrow a⋮2,3,4,6\)\(\Rightarrow a\in BC\left(2,3,4,6\right)\)
mà a phải có giá trị nhỏ nhất ( khi đó \(a+b+c+d+e\)sẽ nhỏ nhất )
\(\Rightarrow a\in BCNN\left(2,3,4,6\right)=12\)
\(\Rightarrow b=12:2=6\), \(c=12:3=4\), \(d=12:4=3\); \(e=12:6=2\)
\(\Rightarrow a+b+c+d+e=12+6+4+3+2=27\)
Vậy giá trị nhỏ nhất có thể có của \(a+b+c+d+e\)là \(27\)