Phương trình : \(3sin3x+\sqrt{3}sin9x=1+4sin^33x\) có nghiệm là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 10 2020
Câu 1:
\(cos^2\) gì nhỉ?
Câu 2: đề không hợp lý \(\sqrt{3}sin9x\) là \(\sqrt{3}cos9x\) có lý hơn
\(\Leftrightarrow3sin3x-4sin^33x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow sin9x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow sin9x=\frac{1}{\sqrt{3}+1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+\frac{k2\pi}{9}\\x=\frac{\pi}{9}-\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+\frac{k2\pi}{9}\end{matrix}\right.\)
Nghiệm nhìn rất ngớ ngẩn nếu đề đúng
3.
\(\Leftrightarrow\frac{1}{2}-\frac{1}{2}cos2x+\frac{\sqrt{3}}{2}sin2x=1\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{6}\right)=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{6}=\frac{\pi}{6}+k2\pi\\2x-\frac{\pi}{6}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
NL
0
LG
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2019
\(sin9x=3sin3x\Leftrightarrow3sin3x-4sin^33x=3sin3x\)
\(\Rightarrow sin^33x=0\Rightarrow sin3x=0\)
\(\Rightarrow3x=k\pi\Rightarrow x=\frac{k\pi}{3}\)
Do \(0\le x\le180\) (đề là \(180\) hay \(180\pi\) đây)
\(\Rightarrow0\le\frac{k\pi}{3}\le180\)
\(\Rightarrow0\le k\le\frac{540}{\pi}\)
\(\Rightarrow0\le k\le171\) (do \(k\in Z\))
Có \(172\) nghiệm
27 tháng 8 2021
1, Phương trình tương đương
\(\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
⇔ \(sin\left(2x-\dfrac{\pi}{6}\right)=1\)
⇔ \(2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k.2\pi\)
⇔ x = \(\dfrac{\pi}{3}+k.\pi\)
2, \(2cos3x+3sin3x-2\)
= \(\sqrt{13}\)\((\dfrac{2}{\sqrt{13}}cos3x+\dfrac{3}{\sqrt{13}}sin3x)\) - 2
Do \(\left(\dfrac{2}{\sqrt{13}}\right)^2+\left(\dfrac{3}{\sqrt{13}}\right)^2=1\) nên tồn tại 1 góc a sao cho \(\left\{{}\begin{matrix}sina=\dfrac{2}{\sqrt{13}}\\cosa=\dfrac{2}{\sqrt{13}}\end{matrix}\right.\)
BT = \(\sqrt{13}sin\left(x+a\right)-2\)
Do - 1 ≤ sin (x + a) ≤ 1 với mọi x và a
⇒ \(-\sqrt{13}-2\le BT\le\sqrt{13}-2\)
⇒ \(-5,6< BT< 1,6\)
Vậy BT nhận 5 giá trị nguyên trong tập hợp S = {-5 ; -4 ; -3 ; -2 ; -1}
3. \(msinx-cosx=\sqrt{5}\)
⇔ \(\dfrac{m}{\sqrt{m^2+1}}.sinx-\dfrac{1}{\sqrt{m^2+1}}.cosx=\dfrac{\sqrt{5}}{\sqrt{m^2+1}}\)
⇔ sin(x - a) = \(\sqrt{\dfrac{5}{m^2+1}}\) với \(\left\{{}\begin{matrix}sina=\dfrac{1}{\sqrt{m^2+1}}\\cosa=\dfrac{m}{\sqrt{m^2+1}}\end{matrix}\right.\)
Điều kiện có nghiệm : \(\left|\sqrt{\dfrac{5}{m^2+1}}\right|\le1\)
⇔ m2 + 1 ≥ 5
⇔ m2 - 4 ≥ 0
⇔ \(\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
CM
11 tháng 7 2018
Chọn A
sin 5 x + sin 9 x + 2 sin 2 x − 1 = 0
⇔ 2 sin 7 x . c o s 2 x − c o s 2 x = 0 ⇔ c o s 2 x = 0 sin 7 x = 1 2
⇔ x = π 4 + k π 2 x = π 42 + k 2 π 7 x = 5 π 42 + k 2 π 7 , k ∈ ℤ
vậy chọn A
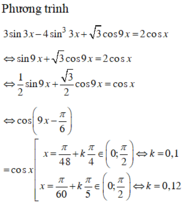
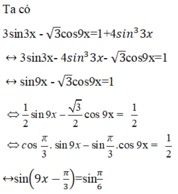
\(3sin3x-4sin^33x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow sin9x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sin9x=1\)
\(\Leftrightarrow sin9x=\frac{1}{\sqrt{3}+1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+k2\pi\\x=\pi-\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+k2\pi\end{matrix}\right.\)