Cho tứ diện ABCD, điểm M ϵ AC, AM = 1/4 AC, N trung điểm AD, cho điểm O trong ΔBCD.
a) MN \(\cap\) (ABO)
b) AO \(\cap\) (MNB)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Kẻ BO cắt CD tại E
Trong mặt phẳng (ACD), nối AE cắt MN tại F
\(\Rightarrow\) F là giao điểm MN và (ABO)
b/ Trong mặt phẳng (ABE) (cũng chính là mặt phẳng (ABO)), nối BF cắt AO tại P
\(\left\{{}\begin{matrix}P\in BF\\BF\in\left(BMN\right)\end{matrix}\right.\) \(\Rightarrow P\in\left(BMN\right)\)
Mà \(P\in AO\Rightarrow AO\cap\left(BMN\right)=P\)


Lời giải:
a) Xét hai tam giác: \(\Delta AEB\) và \(\Delta MED\) có \(AB\text{//}MB:\)
\(\Rightarrow\frac{EA}{EM}=\frac{AB}{MD}\left(1\right)\)
Xét hai tam giác:\(\Delta AFB\) và \(\Delta CFM\) ta có \(AB\text{//}MN:\)
\(\Rightarrow\frac{FA}{FC}=\frac{AB}{MC}\left(2\right)\)
Mà: \(DM=CM\left(gt\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow\frac{EA}{EM}=\frac{FA}{FC}\)
\(\Rightarrow EF\text{//}CM\)
hay \(EF\text{//}DC\left(đpcm\right)\)
Giờ mình làm câu b nha:
Lời giải:
Ta có: \(KN\text{//}CD\Rightarrow KE\text{//}DM\)
\(\Rightarrow\frac{KE}{DM}=\frac{AE}{AM}\left(1\right)\)
Ta lại có: FN//MC
\(\Rightarrow\frac{FN}{MC}=\frac{BF}{BM}\left(2\right)\)
Do EF//AB nên:
\(\Rightarrow\frac{AE}{AM}=\frac{BF}{BM}\left(3\right)\)
Từ \(\left(1\right),\left(2\right)\)và \(\left(3\right)\Rightarrow\frac{KE}{DM}=\frac{FN}{MC}\)
Mà: DM = MC
\(\Rightarrow KE=FN\left(đpcm\right)\)
_Chúc bạn học tốt_

a/ Trong mp (BCD), nối BP cắt CD tại E
Trong mp (ABP), nối MP cắt AE kéo dài tại F (trong trường hợp MP không song song AE)
\(\Rightarrow F=MP\cap\left(ACD\right)\)
b/Nếu MN cắt BC, kéo dài MN cắt BC tại G
Nối GP cắt BD tại H
Trong mặt phẳng (ABD), nối MH cắt AD tại K (trong trường howph MH ko song song AD)
\(\Rightarrow K=AD\cap\left(MNP\right)\)
c/\(H=BD\cap\left(MNP\right)\)

Đáp án B
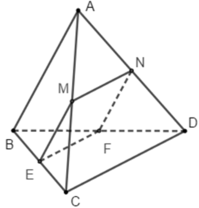
Mặt phẳng α chứa MN song song với AB
Gọi E và F lần lượt là trung điểm của BC và BD
Tam giác ABC có EM là đường trung bình nên ME // = 1/2 AB
Tam giác ABD có FN là đường trung bình nên FN // = 1/2 AB
Suy ra ME // FN // AB và ME = FN
Hay mặt phẳng (MNFE) chính là mặt phẳng α
Vậy thiết diện của mặt phẳng α với tứ diện là hình bình hành MNFE (do ME // = FN)
a/ Trong mặt phẳng (BCD), nối BO kéo dài cắt CD tại E
Trong mặt phẳng (ACD), nối AE cắt MN tại F
\(\Rightarrow F=MN\cap\left(ABO\right)\)
b/ Trong mặt phẳng (ABE), nối BF cắt AO tại P
\(\Rightarrow P=AO\cap\left(MNB\right)\)