Giải phương trình
x\(^3\)- 3x - 52 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
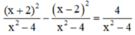
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
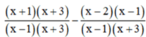
![]()
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)

a.
$x^2-11=0$
$\Leftrightarrow x^2=11$
$\Leftrightarrow x=\pm \sqrt{11}$
b. $x^2-12x+52=0$
$\Leftrightarrow (x^2-12x+36)+16=0$
$\Leftrightarrow (x-6)^2=-16< 0$ (vô lý)
Vậy pt vô nghiệm.
c.
$x^2-3x-28=0$
$\Leftrightarrow x^2+4x-7x-28=0$
$\Leftrightarrow x(x+4)-7(x+4)=0$
$\Leftrightarrow (x+4)(x-7)=0$
$\Leftrightarrow x+4=0$ hoặc $x-7=0$
$\Leftrightarrow x=-4$ hoặc $x=7$
d.
$x^2-11x+38=0$
$\Leftrightarrow (x^2-11x+5,5^2)+7,75=0$
$\Leftrightarrow (x-5,5)^2=-7,75< 0$ (vô lý)
Vậy pt vô nghiệm
e.
$6x^2+71x+175=0$
$\Leftrightarrow 6x^2+21x+50x+175=0$
$\Leftrightarrow 3x(2x+7)+25(2x+7)=0$
$\Leftrightarrow (3x+25)(2x+7)=0$
$\Leftrightarrow 3x+25=0$ hoặc $2x+7=0$
$\Leftrightarrow x=-\frac{25}{3}$ hoặc $x=-\frac{7}{2}$

\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)

a: Khi m=2 thì (1) sẽ là x^2+2x+1=0
=>x=-1
b:x1+x2=52
=>2m-2=52
=>2m=54
=>m=27

`3/(x^2-3x+3)+x^2-3x-3=0`
`<=>3+(x^2-3x-3)(x^2-3x+3)=0`
`<=>3+(x^2-3x)^2-9=0`
`<=>(x^2-3x)^2-6=0`
`<=>x^2-3x=+-6`
Đến đây chia 2 th rồi giải thôi :v
x3 - 3x - 52 = 0
<=> x3 + 4x2 - 4x2 - 16x + 13x - 52 = 0
<=> ( x3 + 4x2 + 13x ) - ( 4x2 + 16x + 52 ) = 0
<=> x( x2 + 4x + 13 ) - 4( x2 + 4x + 13 ) = 0
<=> ( x - 4 )( x2 + 4x + 13 ) = 0
<=> \(\orbr{\begin{cases}x-4=0\\x^2+4x+13=0\end{cases}}\)
+) x - 4 = 0 <=> x = 4
+) x2 + 4x + 13 = ( x2 + 4x + 4 ) + 9 = ( x + 2 )2 + 9 ≥ 9 > 0 ∀ x
Vậy phương trình có nghiệm duy nhất là x = 4