giải phương trình tan3x.tanx = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tan3x.tanx = 1 (Điều kiện: 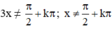 )
)
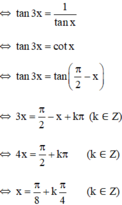
Các nghiệm thuộc họ nghiệm trên đều thỏa mãn điều kiện.
Vậy phương trình có họ nghiệm 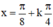 (k ∈ Z).
(k ∈ Z).

a.
\(\Leftrightarrow4cos^32x-3cos2x+3cos2x=\sqrt{2}\)
\(\Leftrightarrow cos^32x=\dfrac{\sqrt{2}}{4}\)
\(\Leftrightarrow cos2x=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow2x=\pm\dfrac{\pi}{4}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{8}+k\pi\) (\(k\in Z\))
c.
ĐKXĐ: \(\left\{{}\begin{matrix}cos3x\ne0\\cosx\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(tan3x.tanx=1\)
\(\Rightarrow tan3x=\dfrac{1}{tanx}\)
\(\Rightarrow tan3x=cotx\)
\(\Rightarrow tan3x=tan\left(\dfrac{\pi}{2}-x\right)\)
\(\Rightarrow3x=\dfrac{\pi}{2}-x+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)

a: ĐKXĐ: sin 2x<>1
=>2x<>pi/2+k2pi
=>x<>pi/4+kpi
\(\dfrac{cos2x}{sin2x-1}=0\)
=>cos2x=0
=>2x=pi/2+kpi
=>x=pi/4+kpi/2
Kết hợp ĐKXĐ, ta được:
x=3/4pi+k2pi hoặc x=7/4pi+k2pi
b: cos(sinx)=1
=>sin x=kpi
=>sin x=0
=>x=kpi
c: \(2\cdot sin^2x-1+cos3x=0\)
=>cos3x+cos2x=0
=>cos3x=-cos2x=-sin(pi/2-2x)=sin(2x-pi/2)
=>cos3x=cos(pi/2-2x+pi/2)=cos(pi-2x)
=>3x=pi-2x+k2pi hoặc 3x=-pi+2x+k2pi
=>x=-pi+k2pi hoặc x=pi/5+k2pi/5
e: cos3x=-cos7x
=>cos3x=cos(pi-7x)
=>3x=pi-7x+k2pi hoặc 3x=-pi+7x+k2pi
=>x=pi/10+kpi/5 hoặc x=pi/4-kpi/2

Nhận thấy tanx=0 không phải nghiệm
\(\Leftrightarrow tan3x=\frac{1}{tanx}\)
\(\Leftrightarrow tan3x=cotx=tan\left(\frac{\pi}{2}-x\right)\)
\(\Rightarrow3x=\frac{\pi}{2}-x+k\pi\)
\(\Rightarrow x=\frac{\pi}{8}+\frac{k\pi}{4}\)
\(\Rightarrow x=\frac{\pi}{8}+\frac{k\pi}{4}\) với \(k=\left\{0;1;2...;7\right\}\)

ta có :
\(\left|x+1\right|+\left|x-1\right|=1+\left|\left(x-1\right)\left(x+1\right)\right|\)
\(\Leftrightarrow\left|x-1\right|\left|x+1\right|-\left|x-1\right|-\left|x+1\right|+1=0\)
\(\Leftrightarrow\left(\left|x-1\right|-1\right)\left(\left|x+1\right|-1\right)=0\Leftrightarrow\orbr{\begin{cases}\left|x-1\right|=1\\\left|x+1\right|=1\end{cases}}\)
\(\Leftrightarrow x\in\left\{-2,0,2\right\}\)

Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)

a: Khi m=2 thì pt sẽ là x^2-6x-3=0
=>\(x=3\pm2\sqrt{3}\)

1. a = 3 thì phương trình trở thành:
\(\frac{x+3}{3-x}-\frac{x-3}{3+x}=\frac{-3\left[3.\left(-3\right)+1\right]}{\left(-3\right)^2}-x^2\)
\(\Leftrightarrow\frac{\left(x+3\right)^2+\left(3-x\right)^2}{\left(3-x\right)\left(3+x\right)}=\frac{-3\left[-9+1\right]}{9}-x^2\)
\(\Leftrightarrow\frac{x^2+6x+9+x^2-6x+9}{\left(3-x\right)\left(3+x\right)}=\frac{-3.\left(-8\right)}{9}-x^2\)
\(\Leftrightarrow\frac{2x^2+18}{9-x^2}=\frac{24}{9}-x^2\)
\(\Leftrightarrow\frac{2x^2+18}{9-x^2}+x^2=\frac{24}{9}\)
\(\Leftrightarrow\frac{2x^2+18+9x^2-x^4}{9-x^2}=\frac{24}{9}\)
\(\Leftrightarrow\frac{11x^2+18-x^4}{9-x^2}=\frac{24}{9}\)
\(\Leftrightarrow99x^2+18-9x^4=216-24x^2\)
\(\Leftrightarrow9x^4-123x^2+198=0\)
Đặt \(x^2=t\left(t\ge0\right)\)
Phương trình trở thành \(9t^2-123t+198=0\)
Ta có \(\Delta=123^2-4.9.198=8001,\sqrt{\Delta}=3\sqrt{889}\)
\(\Rightarrow\orbr{\begin{cases}t=\frac{123+3\sqrt{889}}{18}=\frac{41+\sqrt{889}}{6}\\t=\frac{123-3\sqrt{889}}{18}=\frac{41-\sqrt{889}}{6}\end{cases}}\)
Lúc đó \(\orbr{\begin{cases}x^2=\frac{41+\sqrt{889}}{6}\\x^2=\frac{41-\sqrt{889}}{6}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\pm\sqrt{\frac{41+\sqrt{889}}{6}}\\x=\pm\sqrt{\frac{41-\sqrt{889}}{6}}\end{cases}}\)
Vậy pt có 4 nghiệm \(S=\left\{\pm\sqrt{\frac{41+\sqrt{889}}{6}};\pm\sqrt{\frac{41-\sqrt{889}}{6}}\right\}\)


ĐKXĐ: \(\left\{{}\begin{matrix}cos3x\ne0\\cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\frac{sin3x.sinx}{cos3x.cosx}=1\)
\(\Leftrightarrow sin3x.sinx-cos3x.cosx=0\)
\(\Leftrightarrow sin2x=0\)
\(\Leftrightarrow2sinx.cosx=0\)
\(\Leftrightarrow sinx=0\Leftrightarrow x=k\pi\)