Cho đường tròn (O) tiếp xúc với 2 cạnh Ax, Ay của góc xAy lần lượt tại B và C. Vẽ qua C đường thẳng song song với Ax cắt (O) tại D; AD cắt cung BC nhỏ tại M; CM cắt AB tại N. Chứng minh rằng:
a) Hai tam giác ANC và MNA đồng dạng.
b) AN = BN.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.xét tam giác ANC và tam giác MNA, có:
N: góc chung
góc MAN = góc ACN
=> tam giác ANC đồng dạng tam giác MNA ( g.g )
b.ta có:
\(\dfrac{AN}{MN}=\dfrac{NC}{AN}\) ( tỉ số đồng dạng )
\(\Rightarrow AN^2=MN.NC\)
ta lại có: tam giác BCN đồng dạng tam giác MBN
\(\Rightarrow BN^2=MN.NC\)
=> AN = BN

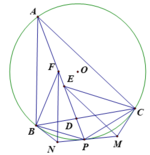
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.