Gpt:x2 +4x2/(x+2)2=12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1 2016
\(\Leftrightarrow x^2-x-2x+2=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\int^{x=1}_{x=2}\)
HG
1
TN
19 tháng 5 2016
x2(x+2)2+4x2=12(x+2)2
=>x2(x+2)2+4x2-12(x+2)2=0
VT=(x2-2x-4)(x2+6x+12)
pt trở thành (x2-2x-4)(x2+6x+12)=0
=>x2-2x-4=0 hoặc x2+6x+12=0
Th1:x2-2x-4=0
denta:(-2)2-(-4(1.4))=20
x1:(2+\(\sqrt{20}\)):2=1+\(\sqrt{5}\)
x2:(2-\(\sqrt{20}\)):2=\(\sqrt{5}\)+1
Th2:x2+6x+12=0
denta:62-4(1.12)=-12
=>\(\Delta< 0\)
=>vô nghiệm
vậy pt có nghiệm là 1-\(\sqrt{5}\)và \(\sqrt{5}\)+1
DN
3
4 tháng 9 2021
\(\left(x^2+x\right)^2+4x^2+4x-12=\left[\left(x^2+x\right)^2+4\left(x^2+x\right)+4\right]-16=\left(x^2+x+2\right)-4^2=\left(x^2+x+2-4\right)\left(x^2+x+2+4\right)=\left(x^2+x-2\right)\left(x^2+x+6\right)=\left(x-1\right)\left(x+2\right)\left(x^2+x+6\right)\)
LN
4 tháng 9 2021
\(\left(x^2+x\right)^2+4x^2+4x-12\\ =\left(x^2+x+2\right)-4\\ =\left(x^2+x-2\right)\left(x^2+x+6\right)\)
CM
13 tháng 8 2017
X é t p h ư ơ n g t r ì n h 1 t a c ó x + 2 3 + x - 3 3 = 0 1 x + 2 3 - 3 - x 3 = 0 x + 2 3 = 3 - x 3 x + 2 = 3 - x 2 x = 1 x = 1 2 X é t p h ư ơ n g t r ì n h 2 t a c ó x 2 + x - 1 2 + 4 x 2 + 4 x = 0 2 x 2 + x - 1 2 + 4 x 2 + 4 x - 4 + 4 = 0 x 2 + x - 1 2 + 4 x 2 + x - 1 + 4 = 0 x 2 + x - 1 + 2 2 = 0 x 2 + x + 1 2 = 0 x 2 + x + 1 = 0 x 2 + x + 1 4 + 3 4 = 0 x + 1 2 2 + 3 4 = 0 V ì x + 1 2 2 + 3 4 > 0 , ∀ x n ê n p h ư ơ n g t r ì n h 2 v ô n g h i ệ m
Vậy Phương trình (1) có 1 nghiệm, phương trình (2) vô nghiệm
Đáp án cần chọn là: D
CM
28 tháng 11 2018
a) MTC = (x -2)(x + 2). Ta rút gọn được M = 1 x − 2
b) Gợi ý: x 2 + 5 x + 6 = ( x + 2 ) ( x + 3 ) ; x 2 + x − 12 = ( x − 3 ) ( x + 4 )
Ta có N = ( x + 2 ) ( x + 3 ) ( x − 3 ) ( x + 4 ) : ( x + 2 ) 2 x ( x − 3 ) = x ( x + 3 ) ( x + 2 ) ( x + 4 )
7 tháng 11 2021
b) x(x-4) - 2x+8 = 0
x(x-4) - 2(x-4) = 0
(x-2) (x-4) = 0
TH1: x-2=0 TH2: x-4=0
x=2 x=4
Vậy x\(\in\){2;4}
7 tháng 11 2021
\(b,\Leftrightarrow\left(x-4\right)\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\\ c,\Leftrightarrow\left(x-5\right)\left(x+5\right)-\left(x+5\right)=0\\ \Leftrightarrow\left(x+5\right)\left(x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-5\end{matrix}\right.\\ d,\Leftrightarrow\left(2x-1\right)^2-\left(2x-1\right)\left(2x+1\right)=0\\ \Leftrightarrow\left(2x-1\right)\left(2x-1-2x-1\right)=0\\ \Leftrightarrow x=\dfrac{1}{2}\\ e,\Leftrightarrow\left(3x-1-x-5\right)\left(3x-1+x+5\right)=0\\ \Leftrightarrow\left(2x-6\right)\left(4x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\\ f,\Leftrightarrow\left(x-2\right)\left(x^2+2x+4\right)-\left(x-2\right)\left(x-12\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x^2+x+16\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{63}{4}=0\left(vô.n_0\right)\end{matrix}\right.\\ \Leftrightarrow x=2\)
23 tháng 9 2021
c: Ta có: \(\left(x+3\right)^3-x\left(3x+1\right)^2+\left(2x+1\right)\left(4x^2-2x+1\right)=28\)
\(\Leftrightarrow x^3+9x^2+27x+27-9x^3-6x^2-x+8x^3+1=28\)
\(\Leftrightarrow3x^2+26x=0\)
\(\Leftrightarrow x\left(3x+26\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{26}{3}\end{matrix}\right.\)
23 tháng 9 2021
\(a,\Leftrightarrow x^2+8x+16-x^3-12x^2=16\\ \Leftrightarrow x^3+11x^2-8x=0\\ \Leftrightarrow x\left(x^2+11x-8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^2+11x-8=0\left(1\right)\end{matrix}\right.\\ \Delta\left(1\right)=121+32=153\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-11-3\sqrt{17}}{2}\\x=\dfrac{-11+3\sqrt{17}}{2}\end{matrix}\right.\\ S=\left\{0;\dfrac{-11-3\sqrt{17}}{2};\dfrac{-11+3\sqrt{17}}{2}\right\}\)
\(c,\Leftrightarrow x^3+9x^2+27x+27-9x^3-6x^2-x+8x^3+1=28\\ \Leftrightarrow3x^2+26x=0\\ \Leftrightarrow x\left(3x+26\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{26}{3}\end{matrix}\right.\\ d,\Leftrightarrow x^3-6x^2+12x-8-x^3-125-6x^2=11\\ \Leftrightarrow-12x^2+12x-144=0\\ \Leftrightarrow x^2-x+12=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=3\end{matrix}\right.\)
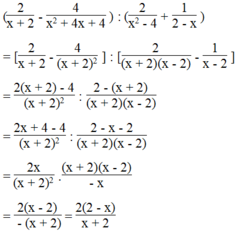
Bài làm:
Ta có: \(\frac{x^2+4x^2}{\left(x+2\right)^2}=12\)
\(\Leftrightarrow5x^2=12\left(x^2+4x+4\right)\)
\(\Leftrightarrow7x^2+48x+48=0\)
\(\Leftrightarrow7\left(x^2+\frac{48}{7}x+\frac{576}{49}\right)-\frac{240}{7}=0\)
\(\Leftrightarrow\left(x+\frac{24}{7}\right)^2-\left(\frac{4\sqrt{15}}{7}\right)^2=0\)
\(\Leftrightarrow\left(x+\frac{24-4\sqrt{15}}{7}\right)\left(x+\frac{24+4\sqrt{15}}{7}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{4\sqrt{15}-24}{7}\\x=-\frac{24+4\sqrt{15}}{7}\end{cases}}\)
*Bổ sung : Thiếu ĐK rồi : \(x\ne-2\)